Кривая Коха

Кривая Коха

Кривая Коха — фрактальная кривая, описанная в 1904 году шведским математиком Хельге фон Кохом.

Три копии кривой Коха, построенные (остриями наружу) на сторонах правильного треугольника, образуют замкнутую кривую потенциально бесконечной длины, называемую снежинкой Коха.

Построение

Кривая Коха является типичным геометрическим фракталом. Процесс её построения выглядит следующим образом: берём единичный отрезок, разделяем на три равные части и заменяем средний интервал равносторонним треугольником без этого сегмента. В результате образуется ломаная, состоящая из четырех звеньев длины 1/3. На следующем шаге повторяем операцию для каждого из четырёх получившихся звеньев и т. д… Предельная кривая и есть кривая Коха.

Пример скрипта(PHP)  

<?php
        set_time_limit(3);
 
        $x = 600;       // Длина рисунка
        $y = 200;       // Высота рисунка
        $r = 10;        // Рамка
        $i = 4;         // Количество итераций
 
        define("PI", 3.14159265358979323846);
 
        $img = imagecreate($x, $y);
        $black = imagecolorallocate($img, 0, 0, 0);
        imagefill($img, 1, 1, $black);
        $color = imagecolorallocate($img, 255, 255, 255);
 
        recursion($i, $r, $y - $r, $x - $r, $y - $r);
        function recursion($i, $x1, $y1, $x2, $y2) {
                global $img, $color;
 
                if($i == 0)
                        imageline($img, $x1, $y1, $x2, $y2, $color);
 
                else {
                        $alpha = atan2($y2 - $y1, $x2 - $x1);
                        $r = sqrt(($x2 - $x1) * ($x2 - $x1) + ($y2 - $y1) * ($y2 - $y1));
 
                        $xa = $x1 + $r * cos($alpha) / 3;
                        $ya = $y1 + $r * sin($alpha) / 3;
 
                        $xc = $xa + $r * cos($alpha - PI / 3) / 3;
                        $yc = $ya + $r * sin($alpha - PI / 3) / 3;
 
                        $xb = $x1 + 2 * $r * cos($alpha) / 3;
                        $yb = $y1 + 2 * $r * sin($alpha) / 3;
 
                        recursion($i - 1, $x1, $y1, $xa, $ya);
                        recursion($i - 1, $xa, $ya, $xc, $yc);
                        recursion($i - 1, $xc, $yc, $xb, $yb);
                        recursion($i - 1, $xb, $yb, $x2, $y2);
                }
        }
 
        header("Content-type: image/png");
        imagepng($img);
        imagedestroy($img);
?>

Снежинка Коха

Свойства

• Кривая Коха нигде не дифференцируема и не спрямляема.
• Кривая Коха не имеет самопересечений.
• Кривая Коха имеет промежуточную (то есть не целую) хаусдорфову размерность, которая равна $\ln4/\ln3\approx 1,26$ поскольку она состоит из четырёх равных частей, каждая из которых подобна всей кривой с коэффициентом подобия 1/3.

Вариации и обобщения

Возможны обобщения кривой Коха, также использующие при построении подстановку ломаной из четырёх равных отрезков, но имеющей иную геометрию. Они имеют хаусдорфову размерность от 1 до 2. В частности, если вместо деления отрезка 1:1:1 использовать золотое сечение (φ:1:φ), то получившаяся кривая имеет отношение к мозаикам Пенроуза.

Также можно построить кривую «Крест Коха» на сторонах квадрата, при этом проводя построение «внутрь» квадрата.

Также можно построить «Снежинку Коха» на сторонах равностороннего трегоугольника.

Вслед за подходом Коха были разработаны варианты с прямыми углами (квадратичная), других углов (Césaro) или кругов и их расширения на высшие размерности (сферическая снежинка):

Вариант	Иллюстрация	Получение
1D, 85°, угол	Фрактал Cesaro	Фрактал Cesaro - вариант кривой Коха с углом между 60° и 90 ° (здесь 85°)
1D, 90°, угол	Квадратичная кривая 1 типа	Первые 2 итерации
1D, 90°, угол	Квадратичная кривая 2 типа	Первые 2 итерации. Фрактальная размерность 1,5 (точно посередине между размерностью 1 и 2), поэтому часто используется при изучении физических свойств нецелых фрактальных объектов
2D, треугольники	Поверхность Коха	Расширения кривой Коха на 2D (первые 3 итерации)
2D, 90°, угол	Квадратичная поверхность 1 типа	Расширение квадратичного кривой 1 типа, соответствующее "вывернутой губке Менгера". На изображении слева - фрактал после второй итерации Квадратичная поверхность (анимация) .
2D, 90°, угол	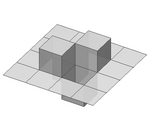Квадратичная поверхность 2 типа	Расширение квадратичного кривой 2 типа. На изображении слева - фрактал после первой итерации
2D, сферы	Haines сферическая снежинка (большой зелёный объект)	Eric Haines разработал фрактал сферическая снежинка, который является трехмерной версией снежинки Коха (используются сферы)

200pm

Ссылки

• Koch Snowflake