Квадратриса
Квадратри́са — плоская трансцендентная кривая, определяемая кинематически. Была предложена в античные времена (V веке до н. э.) для решения задач квадратуры круга и трисекции угла. Квадратриса стала первой в математике трансцендентной кривой[1].


Определение[править | править код]
Кинематическое определение квадратрисы следующее: рассмотрим квадрат (рис. 1), в который вписан сектор четверти круга. Пусть точка равномерно движется по дуге от точки до точки ; одновременно отрезок равномерно движется из положения в положение . Наконец, потребуем, чтобы оба движения начались и закончились одновременно. Тогда точка пересечения радиуса и отрезка опишет квадратрису (см. рисунки 1 и 2, выделена красным цветом).
Античные математики предубеждённо относились к кинематическим определениям кривых, считая их недостойными геометрической науки. Поэтому они предложили два других определения, не использующих понятия механического движения; эти определения приведены в сочинениях Паппа Александрийского и представляют квадратрису как проекцию некоторых кривых, связанных с винтовой линией или спиралью Архимеда[2]. Построения эти довольно сложны и на практике не используются.
В Новое время были обнаружены и другие построения, где возникает квадратриса; например, рассмотрим пересечение витка геликоида с плоскостью, содержащей ось этой поверхности. Тогда проекция линии пересечения на плоскость, перпендикулярную оси, представляет собой ветку квадратрисы[3].
История[править | править код]
Первое упоминание о квадратрисе сделали Папп Александрийский[4] и Ямвлих в конце III века. Папп дал и подробное описание способов её построения. Кривая открыта, по сообщению Прокла Диадоха, софистом Гиппием в V веке до н. э. и использовалась им для решения задачи трисекции угла. Другой античный геометр, Динострат, провёл в IV веке до н. э. исследование этой кривой и показал, что она обеспечивает также решение задачи квадратуры круга. В источниках данную кривую называют «квадратрисой Динострата» или «квадратрисой Гиппия»[5].
Папп пишет, что математик III века Спор Никейский выдвинул два серьёзных возражения против использования квадратрисы для квадратуры круга, с которыми Папп полностью согласен[6]:
- Невозможно точно согласовать движение отрезков ВС и АВ, если не знать заранее отношение длины дуги четверти окружности к радиусу, поэтому получается порочный круг.
- Точку К построить нельзя, потому что в соответствующий момент времени отрезок и радиус совпадают. В современной терминологии, точка К есть предел точек квадратрисы — понятие, чуждое античной математике.
В Новое время кривую исследовали Роберваль (1636), Ферма, Барроу (1670) и другие известные математики. Декарт посвятил исследованию квадратрисы немало страниц в своей «Геометрии» (1637)[7]. Ньютон в 1676 году определил длину дуги квадратрисы, её кривизну и площадь её сегмента в виде ряда, а также указал способ проведения касательных[8].
Уравнения кривой[править | править код]
| Вывод |
|---|
| Пусть — радиус круга, — текущий угол , — полярный радиус. Для удобства введём время , которое за период движения меняется от 0 до 1. Тогда равномерное движение точки по дуге длиной можно выразить уравнением:
Равномерное движение отрезка выражается уравнением: Подставляя значение из первого уравнения во второе, получаем окончательно: |
| Вывод |
|---|
| Приводим уравнение в полярных координатах к виду:
Учитывая , получаем Из геометрических соображений: . Тогда уравнение предстанет в виде: Берём тангенс от обеих частей: то есть |
Основное свойство[править | править код]
Уравнение квадратрисы в полярных координатах можно записать в виде:
- или: где
Отсюда следует основное свойство данной кривой[9]:
|
Ординаты любых двух точек квадратрисы относятся, как полярные углы этих точек: |
Квадратриса — единственная (невырожденная) кривая в первом координатном квадранте, обладающая таким свойством (это легко доказать, повторив приведённые рассуждения в обратном порядке).
Другие свойства[править | править код]
Площадь сегмента квадратрисы определяется формулой[3]:
Применение[править | править код]
Трисекция угла[править | править код]
Трисекция угла, то есть деление произвольного угла на три равные части, с помощью квадратрисы проводится элементарно. Пусть (рис. 1) — некоторый угол, треть которого надо построить. Алгоритм деления следующий:
- Находим точку на квадратрисе и её ординату .
- Откладываем на отрезке его третью часть; получим некоторую точку .
- Находим на квадратрисе точку с ординатой .
- Проводим луч . Угол — искомый.
Доказательство данного алгоритма сразу следует из основного свойства квадратрисы. Очевидно также, что аналогичным способом можно разделить угол не только на три, но и на любое другое число частей[10].
Квадратура круга[править | править код]

Задача квадратуры круга ставится так: построить квадрат с такой же площадью, как у заданного круга радиуса . Алгебраически это означает решение уравнения: .
Построим для исходного круга квадратрису, как на рис. 1. Используя первый замечательный предел, получаем, что абсцисса её нижней точки (на рис. 3 это отрезок ) равна . Выразим это в виде пропорции: , где — длина окружности. Приведённое соотношение позволяет построить отрезок длины . Прямоугольник со сторонами и будет иметь нужную площадь, а построить равновеликий ему квадрат — дело несложное, см. статью Квадратура (математика) или рис. 3.
Вариации[править | править код]
Помимо рассмотренной выше квадратрисы Динострата, существует ряд иных кривых, которые можно использовать для квадратуры круга, и поэтому также называемых квадратрисами[3].
- Квадратриса Озанама:
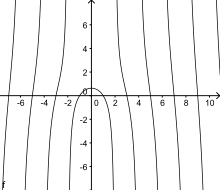
Кроме того, ряд авторов предпочитают поменять местами x и y в уравнении квадратрисы Динострата[12]:
Этот вариант (полная квадратриса) имеет то преимущество, что функция определена на всей вещественной оси, кроме особых точек (В точке функция доопределяется предельным переходом; см. её график при на рис. 4.) В полярных координатах центральная ветка данного варианта кривой описывается формулой[12]:
Данная кривая имеет бесконечное число ветвей, для которых вертикальные прямые в особых точках являются асимптотами. Точки кривой с ординатой (за исключением точки на оси ординат) являются точками перегиба[12].
Примечания[править | править код]
- ↑ История математики. С древнейших времен до начала Нового времени // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I. — С. 84—85.
- ↑ Прасолов В. В., 1992, с. 58—61.
- ↑ 1 2 3 Савелов А. А., 1960, с. 230.
- ↑ Папп Александрийский. Математическое собрание, книга IV, 30—34.
- ↑ Савелов А. А., 1960, с. 227.
- ↑ Прасолов, 2018, с. 71.
- ↑ Прасолов В. В., 1992, с. 61—62.
- ↑ Исаак Ньютон. Математические работы / Перевод и комментарии Д. Д. Мордухай-Болтовского. — М.—Л.: ОНТИ, 1937. — С. 31, 87—89, 99, 166, 227, 287. — 452 с. — (Классики естествознания).
- ↑ Три знаменитые задачи древности, 1963, с. 34—35.
- ↑ Три знаменитые задачи древности, 1963, с. 35—37.
- ↑ 1 2 Вилейтнер Г. История математики от Декарта до середины XIX столетия. — М.: ГИФМЛ, 1960. — С. 284. — 468 с.
- ↑ 1 2 3 Савелов А. А., 1960, с. 228.
Литература[править | править код]
- Жуков А. В. «О числе π» Архивная копия от 29 февраля 2008 на Wayback Machine. М.: МЦНМО, 2002 г., 32 с ISBN 5-94057-030-5
- Прасолов В. В. История математики, в двух томах. — М.: МЦНМО, 2018. — Т. 1. — 296 с. — ISBN 978-5-4439-1275-2, 978-5-4439-1276-9.
- Прасолов В. В. Три классические задачи на построение. Удвоение куба, трисекция угла, квадратура круга. — М.: Наука, 1992. — 80 с. — (Популярные лекции по математике, выпуск 62).
- Прошлецова И. Л. О квадратрисе Динострата // Историко-математические исследования. СПб.: Изд-во Международного фонда истории науки. Вып. 35 (1994). С. 220—229.
- Савелов А. А. Плоские кривые: Систематика, свойства, применения (справочное руководство). — М.: Физматлит, 1960. — С. 227—230. — 293 с. Переиздана в 2002 году, ISBN 5-93972-125-7.
- Чистяков В. Д. Три знаменитые задачи древности. — М.: Гос. уч.-пед. изд-во Министерства просвещения РСФСР, 1963. — С. 33—37. — 96 с.
- Щетников А. И. Как были найдены некоторые решения трёх классических задач древности? // Математическое образование. — 2008. — № 4 (48). — С. 3—15.
- Щетников А. И. Квадратриса Гиппия и её связь с задачами о трисекции угла и о квадратуре круга // Труды VIII Международных Колмогоровских чтений. — Ярославль: Изд-во ЯГПУ, 2010. — С. 392—396. — ISBN 978-5-87555-630-2.
Ссылки[править | править код]
- Quadratrix of Hippias Архивная копия от 4 февраля 2012 на Wayback Machine at the MacTutor archive. (англ.)
- Quadratrix of Hippias at Convergence. (англ.)
Эта статья входит в число добротных статей русскоязычного раздела Википедии. |

























































