Десятиугольник: различия между версиями

Интерактивная навигация по истории

(Показать все непатрулированные изменения)

[отпатрулированная версия]

[непроверенная версия]

← Предыдущая правка Следующая правка →

Содержимое удалено Содержимое добавлено

ВизуальныйВики-текст

Линейный

Версия от 10:56, 5 февраля 2016

Правильный десятиугольник

Рёбер и вершин	10
Символ Шлефли	{10}
Внутренний угол	144°
Симметрия	Диэдрическая ( $D_{10}$ )

Десятиуго́льник (правильный десятиугольник — декагон) — многоугольник с десятью углами и десятью сторонами.

Правильный десятиугольник

У правильного десятиугольника все стороны равной длины и каждый внутренний угол составляет 144°.

Площадь правильного десятиугольника равна (t - длина стороны):

$A={\frac {5}{2}}t^{2}\cot {\frac {\pi }{10}}={\frac {5t^{2}}{2}}{\sqrt {5+2{\sqrt {5}}}}\simeq 7.694t^{2}.$

Альтернативная формула $A=2.5dt$ , где d - расстояние между параллельными сторонами или диаметр вписанной окружности. В тригонометрических функциях он выражается так:

$d=2t\left(\cos {\tfrac {3\pi }{10}}+\cos {\tfrac {\pi }{10}}\right),$

и может быть представлен в радикалах как

$d=t{\sqrt {5+2{\sqrt {5}}}}.$

Сторона правильного десятиугольника, вписанного в единичную окружность, равна ${\tfrac {{\sqrt {5}}-1}{2}}={\tfrac {1}{\varphi }}$ , где $\varphi$ - золотое сечение.

Построение

По теореме Гаусса - Ванцеля правильный десятиугольник возможно построить, используя лишь циркуль и линейку.

Иначе его можно построить следующим образом:

Построить сначала правильный пятиугольник.
Соединить все его вершины с центром описанной окружности прямыми до пересечения с этой же окружностью на противоположной стороне. В этих точках пересечения и находятся остальные пять вершин десятиугольника.
Соединить по порядку вершины пятиугольника и пять точек, найденный шагом ранее. Искомый десятиугольник построен.

Разбиение правильного десятиугольника

Гарольдом Коксетером было доказано, что правильный 2m-угольник можно разбить на m(m-1)/2 ромбов. Для декагона m=5, так что он может быть разбит на 10 ромбов.

Разбиение правильного десятиугольника

Пространственный десятиугольник

Правильные пространственные декагоны
{5}#{ }	{5/2}#{ }	{5/3}#{ }

Пространственный десятиугольник - это пространственный многоугольник с десятью рёбрами и вершинами, но не лежащими в одной плоскости. У пространственного зиг-заг десятиугольника вершины чередуются между двумя параллельными плоскостями.

У правильного пространственного декагона все рёбра равны. В трёхмерном пространстве это зиг-заг пространственный декагон, он может быть обнаружен среди рёбер и вершин пентагональной антипризмы, пентаграммной антипризмы, пентаграммной перекрещивающейся антипризмы с той же D_5d [2⁺,10] симметрией порядка 20.

Его также можно найти в некоторых выпуклых многогранниках с икосаэдрической симметрией. Многоугольники по периметру этих проекций (см. ниже) это пространственные декагоны.

Ортогональные проекции многогранников
Додекаэдр	Икосаэдр	Икосододекаэдр	Ромботриаконтаэдр

Внешние ссылки

Weisstein, Eric W. Decagon (англ.) на сайте Wolfram MathWorld.
На Викискладе есть медиафайлы по теме Десятиугольник

@@ Строка 4: / Строка 4: @@
 |align=center colspan=2|[[Файл:Regular decagon.svg|200px]]
 |-
+|Рёбер и вершин
-|bgcolor=#e7dcc3|Рёбра и вершины||10
+|10
 |-
+|Символ Шлефли
-|bgcolor=#e7dcc3|[[Площадь]]||<math>A = \frac{5}{2}t^2 \cot \frac{\pi}{10}</math><math> = \frac{5t^2}{2} \sqrt{5+2\sqrt{5}}</math> <math> \simeq 7.694208843 t^2.</math>
+|{10}
 |-
-|bgcolor=#e7dcc3|[[Внутренний угол]] (градусы)||144°
+|Внутренний угол
+|144°
+|-
+|Симметрия
+|Диэдрическая (<math> D_{10}</math>)
 |}
-'''Десятиуго́льник''' (правильный десятиугольник — декагон) — [[многоугольник]] с десятью углами.
+'''Десятиуго́льник''' (правильный десятиугольник — декагон) — [[многоугольник]] с десятью углами и десятью сторонами.
+== Правильный десятиугольник ==
-Площадь правильного десятиугольника вычисляется следующим образом:
+У правильного десятиугольника все стороны равной длины и каждый внутренний угол составляет 144°.
-: <math>
-  A = \frac{5}{2}a^2 \cot \frac{\pi}{10} =
+Площадь правильного десятиугольника равна (t - длина стороны):
-\frac{5a^2}{2} \sqrt{5+2\sqrt{5}} \simeq 7.694208843\, a^2.
- </math>
+<math> A = \frac{5}{2}t^2 \cot \frac{\pi}{10} = \frac{5t^2}{2} \sqrt{5+2\sqrt{5}} \simeq 7.694 t^2.</math>
-[[File:Regular Decagon Inscribed in a Circle.gif|Construction of a regular decagon]]
+Альтернативная формула <math> A=2.5dt</math>, где d - расстояние между параллельными сторонами или диаметр вписанной окружности. В тригонометрических функциях он выражается так:
+<math> d=2t\left(\cos\tfrac{3\pi}{10}+\cos\tfrac{\pi}{10}\right),</math>
+и может быть представлен в радикалах как
+<math> d=t\sqrt{5+2\sqrt{5}}.</math>
+Сторона правильного десятиугольника, вписанного в единичную окружность, равна <math> \tfrac{\sqrt{5}-1}{2}=\tfrac{1}{\varphi}</math>, где <math> \varphi</math> - [[золотое сечение]].
+=== Построение ===
+По [[Теорема Гаусса — Ванцеля|теореме Гаусса - Ванцеля]] правильный десятиугольник возможно построить, используя лишь циркуль и линейку.
+[[Файл:Regular_Decagon_Inscribed_in_a_Circle.gif|none|thumb|314x314px|Построение правильного десятиугольника]]
+Иначе его можно построить следующим образом:
+# Построить сначала [[правильный пятиугольник]].
+# Соединить все его вершины с центром описанной окружности прямыми до пересечения с этой же окружностью на противоположной стороне. В этих точках пересечения и находятся остальные пять вершин десятиугольника.
+# Соединить по порядку вершины пятиугольника и пять точек, найденный шагом ранее. Искомый десятиугольник построен.
+== Разбиение правильного десятиугольника ==
+[[Коксетер, Гарольд|Гарольдом Коксетером]] было доказано, что правильный 2m-угольник можно разбить на m(m-1)/2 ромбов. Для декагона m=5, так что он может быть разбит на 10 ромбов.
+{| class="wikitable"
+! colspan="2" |Разбиение правильного десятиугольника
+|-
+|[[Файл:Rhombic dissected decagon.png|centre|frameless|157x157px]]
+|[[Файл:Rhomb dissected dodecagon2.png|centre|frameless|156x156px]]
+|}
+== Пространственный десятиугольник ==
+{| class="wikitable" align="right" width="300"
+! colspan="3" |Правильные пространственные декагоны
+|-
+!{5}#{ }
+!{5/2}#{ }
+!{5/3}#{ }
+|-
+|[[File:Regular_skew_polygon_in_pentagonal_antiprism.png|link=https://en.wikipedia.org/wiki/File:Regular_skew_polygon_in_pentagonal_antiprism.png|100x100px]]
+|[[File:Regular_skew_polygon_in_pentagrammic_antiprism.png|link=https://en.wikipedia.org/wiki/File:Regular_skew_polygon_in_pentagrammic_antiprism.png|107x107px]]
+|[[File:Regular_skew_polygon_in_pentagrammic_crossed-antiprism.png|link=https://en.wikipedia.org/wiki/File:Regular_skew_polygon_in_pentagrammic_crossed-antiprism.png|100x100px]]
+|}
+'''Пространственный десятиугольник''' - это [[пространственный многоугольник]] с десятью рёбрами и вершинами, но не лежащими в одной плоскости. У ''пространственного зиг-заг десятиугольника'' вершины чередуются между двумя параллельными плоскостями.
+У правильного пространственного декагона все рёбра равны. В трёхмерном пространстве это зиг-заг пространственный декагон, он может быть обнаружен среди рёбер и вершин пентагональной антипризмы, пентаграммной антипризмы, пентаграммной перекрещивающейся антипризмы с той же D<sub>5d</sub> [2<sup>+</sup>,10] симметрией порядка 20.
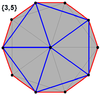
+Его также можно найти в некоторых [[Выпуклый многогранник|выпуклых многогранниках]] с икосаэдрической симметрией. Многоугольники по периметру этих проекций (см. ниже) это пространственные декагоны.
+{| class="wikitable" width="500"
+|+
+Ортогональные проекции многогранников
+|[[File:Dodecahedron_petrie.png|link=https://en.wikipedia.org/wiki/File:Dodecahedron_petrie.png|100x100px]][[Додекаэдр]]
+|[[File:Icosahedron_petrie.png|link=https://en.wikipedia.org/wiki/File:Icosahedron_petrie.png|100x100px]][[Икосаэдр]]
+|[[File:Dodecahedron_t1_H3.png|link=https://en.wikipedia.org/wiki/File:Dodecahedron_t1_H3.png|100x100px]][[Икосододекаэдр]]
+|[[File:Dual_dodecahedron_t1_H3.png|link=https://en.wikipedia.org/wiki/File:Dual_dodecahedron_t1_H3.png|102x102px]][[Ромботриаконтаэдр]]
+|}
 == Внешние ссылки ==

Символ Шлефли
Многоугольники	{1} {2} {3} {4} {5} {6} {7} {8} {9} {10} {11} {12} {13} {14} {15} {16} {17} {18} {19} {20} {24} {30} {257} {65537} {1000000} {4294967295} {∞}
Звёздчатые многоугольники	{5/2} {6/2} {7/2} {7/3} {8/2} {8/3} {9/2} {9/3} {9/4}
Паркеты на плоскости	{3,6} {4,4} {6,3}
Правильные многогранники и сферические паркеты	{2,n} {3,3} {4,3} {3,4} {5,3} {3,5} {n,2}
Многогранники Кеплера — Пуансо	{5/2,5} {5,5/2} {5/2,3} {3,5/2}
Соты	{4,3,4}
Четырёхмерные многогранники	{3,3,3} {4,3,3} {3,3,4} {3,4,3} {5,3,3} {3,3,5}

Десятиугольник: различия между версиями

Версия от 10:56, 5 февраля 2016

Содержание

Правильный десятиугольник

Построение

Разбиение правильного десятиугольника

Пространственный десятиугольник

Внешние ссылки

Навигация

Десятиугольник: различия между версиями

Версия от 10:56, 5 февраля 2016

Правильный десятиугольник

Построение

Разбиение правильного десятиугольника

Пространственный десятиугольник

Внешние ссылки

Навигация

Поиск