Восемнадцатиугольник
| Восемнадцатиугольник | |
|---|---|
 Правильный восемнадцатиугольник | |
| Тип | Правильный многоугольник |
| Рёбра | |
| Символ Шлефли | , |
| Диаграмма Коксетера — Дынкина |
|
| Вид симметрии | Диэдрическая группа , порядок 2×18 |
| Внутренний угол | |
| Свойства | |
| выпуклый, вписанный, равносторонний, равноугольный, изотоксальный | |
Восемнадцатиугольник — многоугольник с восемнадцатью сторонами[1].
Правильный восемнадцатиугольник[править | править код]
Правильный восемнадцатиугольник имеет символ Шлефли и может быть построен как полуправильный усечённый девятиугольник, , в котором перемежаются два типа сторон.
Построение[править | править код]
Имея сторон, правильный восемнадцатиугольник не может быть построен с помощью циркуля и линейки по теореме Гаусса — Ванцеля[2]. Однако его можно построить с помощью невсиса или трисекции угла с использованием томагавка.

Следующее приближённое построение очень близко к построению девятиугольника, поскольку восемнадцатиугольник, как уже было сказано выше, может быть построен путём усечения девятиугольника. Данное построение возможно сделать с помощью только циркуля и линейки.

|
Симметрия[править | править код]

Правильный восемнадцатиугольник имеет диэдральную группу порядка . Имеется типов подгрупп диэдральной симметрии: , (, ) и (, ), а также 6 циклических групп симметрии: (, ), (, ) и (, ).
На рисунке справа можно видеть подгрупп симметрии восемнадцатиугольника. Конвей использовал для их обозначения буквы вместе с порядком группы[3]. Полная симметрия правильной фигуры будет равна , а отсутствие симметрии (то есть тривиальная группа) отмечается как . Диэдральные симметрии делятся по тому, проходят ли их оси через вершины (используется буква , от «diagonal») или через середины сторон (используется буква , от «perpendicular»). Если же оси симметрии проходят и через вершины, и через середины сторон, используется буква . Циклические группы отмечаются буквой (от «gyration»).
Все эти подгруппы могут являться диэдральными группами неправильных восемнадцатиугольников, и лишь подгруппа не даёт свободы в этом отношении, если только стороны многоугольника не рассматриваются как имеющие направление, то есть как векторы.
Использование[править | править код]
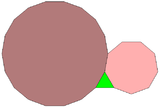
Правильные треугольник, девятиугольник и восемнадцатиугольник могут полностью окружить точку на плоскости, являясь одной из 17 комбинаций правильных многоугольников с таким свойством[4]. Однако эта комбинация не может быть использована для архимедова замощения плоскости — треугольник и девятиугольник имеют нечётное число сторон, ни одна из этих фигур не может быть окружена чередующимися другими двумя типами многоугольников.
Правильные восемнадцатиугольники могут замощать плоскость, оставляя вогнутые шестиугольные бреши. Другое замощение использует девятиугольники и невыпуклые восьмиугольники. Путём сокращения некоторых вершин первая мозаика может быть превращена в усечённую шестиугольную мозаику, а вторая — в усечённую тришестиугольную мозаику.
Другие восемнадцатиугольники фигуры[править | править код]
Звёздчатые -угольники имеют символы . Существует два правильных звёздчатых многоугольника: и . Они используют те же самые вершины, но соединяют каждую пятую или седьмую вершину. Имеются также составные восемнадцатиугольники: эквивалентен (двум девятиугольникам), эквивалентен (трём шестиугольникам), и эквивалентны и (двум эннеаграммам), эквивалентен ( равносторонним треугольникам), и, наконец, эквивалентен (девять двуугольников).
| Составные и звёздчатые многоугольники | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Вид | Выпуклый многоугольник | Составные | Звёздчатый многоугольник | Составной | Звёздчатый многоугольник | Составной | |||
| Рисунок |  = |
 = |
 = |
 = |
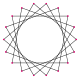 |
 = |
 |
 = |
 = |
| Внутренний угол | |||||||||
Более глубокие усечения правильного многоугольника и правильной эннеаграммы дают равноугольные (вершинно-транзитивные) промежуточные восемнадцатиугольники с находящимися на равном расстоянии вершинами и двумя длинами сторон. Другие усечения дают двойное покрытие: [5].
| Вершинно-транзитивные усечения девятиугольника и эннеаграмм | |||||
|---|---|---|---|---|---|
| Квазиправильные | Изогональные | Квазиправильные Двойное покрытие | |||
 |

|
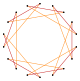
|

|

|
 |
 |

|

|
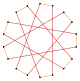
|

|
 |
 |
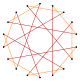
|

|

|

|
 |
Многоугольники Петри[править | править код]
Правильный восемнадцатиугольник является многоугольником Петри для ряда политопов, что показано в косоортогональных проекциях на плоскость Коксетера:
| Восемнадцатиугольные многоугольники Петри | |||||||
|---|---|---|---|---|---|---|---|
| A17 | B9 | D10 | E7 | ||||
 17-симплекс |
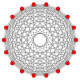 9-ортогранник |
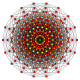 Эннеракт |
 711 |
 171 |
 321 |
 231 |
 >132 |
Примечания[править | править код]
- ↑ Adams, 1907, с. 528.
- ↑ Conway, 2010, с. 31.
- ↑ Conway, Burgiel, Goodman-Strauss, 2008, с. 275-278.
- ↑ Dallas, 1855, с. 134.
- ↑ Grünbaum, 1994, с. 35-48.
Литература[править | править код]
- Henry Adams. Cassell's Engineer's Handbook: Comprising Facts and Formulæ, Principles and Practice, in All Branches of Engineering. — D. McKay, 1907. — С. 528.
- John B. Conway. Mathematical Connections: A Capstone Course. — American Mathematical Society, 2010. — С. 31. — ISBN 9780821849798.
- L. Christine Kinsey, Teresa E. Moore. Symmetry, Shape, and Surfaces: An Introduction to Mathematics Through Geometry. — Springer, 2002. — С. 86. — ISBN 9781930190092.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss. Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon // The Symmetries of Things. — Wellesley, MA: A K Peters, Ltd., 2008. — ISBN 978-1-56881-220-5.
- Branko Grünbaum. The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History / Richard K.Guy, Robert E. Woodrow. — The Mathematical Association of America, 1994. — (MAA Spectrum). — ISBN 0-88385-516-X.
- Elmslie William Dallas. The Elements of Plane Practical Geometry, Etc. — John W. Parker & Son, 1855.
Ссылки[править | править код]
- Weisstein, Eric W. Octadecagon (англ.) на сайте Wolfram MathWorld.
Для улучшения этой статьи желательно:
|






















































































