Кривая Коха

Кривая Коха

Кривая Коха — фрактальная кривая, описанная в 1904 году шведским математиком Хельге фон Кохом.

Три копии кривой Коха, построенные (остриями наружу) на сторонах правильного треугольника, образуют замкнутую кривую бесконечной длины, называемую снежинкой Коха.

Построение

Кривая Коха является типичным геометрическим фракталом. Процесс её построения выглядит следующим образом: берём единичный отрезок, разделяем на три равные части и заменяем средний интервал равносторонним треугольником без этого сегмента. В результате образуется ломаная, состоящая из четырёх звеньев длины 1/3. На следующем шаге повторяем операцию для каждого из четырёх получившихся звеньев и т. д… Предельная кривая и есть кривая Коха.

Пример скрипта (PHP)

<?php
        $i = 4;
        
        $image = imagecreatetruecolor(600, 200);
        imagefilledrectangle($image, 0, 0, imagesx($image) - 1, imagesy($image) - 1,
                imagecolorresolve($image, 255, 255, 255));
        $color = imagecolorresolve($image, 0, 0, 0);
 
        drawKoch($image, 0, imagesy($image) - 1, imagesx($image), imagesy($image) - 1, $i, $color);
        
        /**
         * Draws koch curve between two points.
         * @return void
         */
        function drawKoch($image, $xa, $ya, $xe, $ye, $i, $color) {
            if($i == 0)
                imageline($image, $xa, $ya, $xe, $ye, $color);
            else {
                //       C
                //      / \
                // A---B   D---E
                
                $xb = $xa + ($xe - $xa) * 1/3;
                $yb = $ya + ($ye - $ya) * 1/3;

                $xd = $xa + ($xe - $xa) * 2/3;
                $yd = $ya + ($ye - $ya) * 2/3;

                $cos60 = 0.5;
                $sin60 = -0.866;
                $xc = $xb + ($xd - $xb) * $cos60 - $sin60 * ($yd - $yb);
                $yc = $yb + ($xd - $xb) * $sin60 + $cos60 * ($yd - $yb);

                drawKoch($image, $xa, $ya, $xb, $yb, $i - 1, $color);
                drawKoch($image, $xb, $yb, $xc, $yc, $i - 1, $color);
                drawKoch($image, $xc, $yc, $xd, $yd, $i - 1, $color);
                drawKoch($image, $xd, $yd, $xe, $ye, $i - 1, $color);
            }
        }
 
        header('Content-type: image/png');
        imagepng($image);
        imagedestroy($image);
?>

Пример прямоугольной кривой (Pascal)

uses crt, graph;
var
a,b,i:integer;

procedure drawline(ax,ay,fx,fy,i: integer);
var
bx,by,cx,cy,dx,dy,ex,ey:integer;
begin
if (i=0) or keypressed then
   line(ax,ay,fx,fy)
else
    begin
    bx:=(2*ax+fx) div 3;
    by:=(2*ay+fy) div 3;
    cx:=bx+by-ay;
    cy:=by+ax-bx;
    ex:=2*bx-ax;
    ey:=2*by-ay;
    if ax = fx then
       begin
       dx:=cx;
       dy:=ey;
       end
    else
        begin
        dx:=ex;
        dy:=cy;
        end;
    drawline(ax,ay,bx,by,i-1);
    drawline(bx,by,cx,cy,i-1);
    drawline(cx,cy,dx,dy,i-1);
    drawline(dx,dy,ex,ey,i-1);
    drawline(ex,ey,fx,fy,i-1);
    end;
end;

begin
i:=6;
a:=detect;
initgraph(a,b,'');
setbkcolor(15);
setcolor(red);
cleardevice;
outtextxy(0,0,'Wait...');
drawline(0,getmaxy, getmaxx, getmaxy, i);
outtextxy(0,20,'Sucsessful! Press any key...');
if keypressed then readkey;
readkey;
closegraph;
end.

Снежинка Коха

Свойства

• Кривая Коха нигде не дифференцируема и не спрямляема.
• Кривая Коха имеет бесконечную длину.
• Кривая Коха не имеет самопересечений.
• Кривая Коха имеет промежуточную (то есть не целую) хаусдорфову размерность, которая равна $\ln 4/\ln 3\approx 1,26$ поскольку она состоит из четырёх равных частей, каждая из которых подобна всей кривой с коэффициентом подобия 1/3.

Вариации и обобщения

Возможны обобщения кривой Коха, также использующие при построении подстановку ломаной из четырёх равных отрезков, но имеющей иную геометрию. Они имеют хаусдорфову размерность от 1 до 2. В частности, если вместо деления отрезка 1:1:1 использовать золотое сечение (φ:1:φ), то получившаяся кривая имеет отношение к мозаикам Пенроуза.

Также можно построить «Снежинку Коха» на сторонах равностороннего трегоугольника.

Вслед за подходом Коха были разработаны варианты с прямыми углами (квадратичная), других углов (Césaro) или кругов и их расширения на высшие размерности (сферическая снежинка):

Вариант	Иллюстрация	Получение
1D, 85°, угол	Фрактал Cesaro	Фрактал Cesaro — вариант кривой Коха с углом между 60° и 90 ° (здесь 85°)
1D, 90°, угол	Квадратичная кривая 1 типа	Первые 2 итерации
1D, 90°, угол	Квадратичная кривая 2 типа	Первые 2 итерации. Фрактальная размерность 1,5 (точно посередине между размерностью 1 и 2), поэтому часто используется при изучении физических свойств нецелых фрактальных объектов
2D, треугольники	Поверхность Коха	Расширения кривой Коха на 3D (первые 3 итерации)
2D, 90°, угол	Квадратичная поверхность 1 типа	Расширение квадратичного кривой 1 типа, соответствующее «вывернутой губке Менгера». На изображении слева — фрактал после второй итерации Квадратичная поверхность (анимация) .
2D, 90°, угол	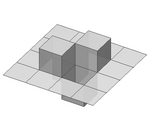Квадратичная поверхность 2 типа	Расширение квадратичного кривой 2 типа. На изображении слева — фрактал после первой итерации
2D, сферы	Haines сферическая снежинка (большой зелёный объект)	Eric Haines разработал фрактал сферическая снежинка, который является трехмерной версией снежинки Коха (используются сферы)

Снежинка Коха

Снежинка Коха, построенная в виде замкнутой кривой на базе равностороннего треугольника, впервые была описана шведским математиком Хельге фон Кохом в 1904 году. Было доказано, что она обладает рядом любопытных свойств, например её периметр имеет бесконечную длину, что однако не мешает ему охватывать конечную площадь. Вычисление фрактальной размерности снежинки Коха даёт значение приблизительно равное 1,26.

Ссылки

• Koch Snowflake