Фигуры Лиссажу: различия между версиями
| [непроверенная версия] | [отпатрулированная версия] |
/* Математическое выражение для кривой Лижу |
Д.Ильин (обсуждение | вклад) м откат правок 178.120.1.82 (обс) к версии VladVD |
||
| Строка 1: | Строка 1: | ||
[[Файл:Lissajous.svg|300px|right|Фигуры Лиссажу]] |
|||
| ⚫ | |||
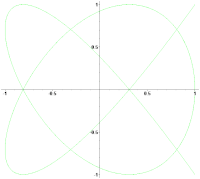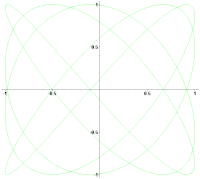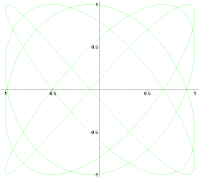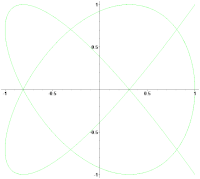
'''Фигу́ры Лиссажу́''' — [[Замкнутая траектория|замкнутые траектории]], прочерчиваемые точкой, совершающей одновременно два [[Гармонические колебания|гармонических колебания]] в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёным [[Лиссажу, Жюль Антуан|Жюлем Антуаном Лиссажу]]. Вид фигур зависит от соотношения между [[Период колебаний|периодами]] ([[Частота периодического процесса|частотами]]), фазами и [[Амплитуда|амплитудами]] обоих колебаний. В простейшем случае равенства обоих периодов фигуры представляют собой эллипсы, которые при разности фаз 0 или <math>\pi</math> вырождаются в отрезки прямых, а при разности фаз <math>\frac{\pi}{2}</math> и равенстве амплитуд превращаются в окружность. Если периоды обоих колебаний неточно совпадают, то разность фаз всё время меняется, вследствие чего эллипс всё время деформируется. При существенно различных периодах фигуры Лиссажу не наблюдаются. Однако, если периоды относятся как целые числа, то через промежуток времени, равный наименьшему кратному обоих периодов, движущаяся точка снова возвращается в то же положение — получаются фигуры Лиссажу более сложной формы. Фигуры Лиссажу вписываются в прямоугольник, центр которого совпадает с началом [[Координаты|координат]], а стороны параллельны осям координат и расположены по обе стороны от них на расстояниях, равных амплитудам колебаний. |
|||
== Математическое выражение для кривой Лиссажу == |
|||
фцлвтавуыфла |
|||
лщжщдтлжоДЛ дщ |
|||
<math>\left\{ \begin{align} |
|||
т |
|||
& x(t)=A\sin (at+\delta ) \\ |
|||
& y(t)=B\sin (bt) \\ |
|||
\end{align} \right.</math> |
|||
где ''A'', ''B'' — амплитуды колебаний, ''a'', ''b'' — частоты, ''δ'' — сдвиг фаз |
|||
д |
|||
Вид кривой сильно зависит от соотношения ''a''/''b''. Когда соотношение равно 1, фигура Лиссажу имеет вид эллипса, при определённых условиях она имеет вид [[Окружность|окружности]] (''A'' = ''B'', ''δ'' = [[Пи (число)|π]]/2 [[радиан]]) и отрезка [[прямая|прямой]] (''δ'' = 0). |
|||
ТИ |
|||
Ещё один пример фигуры Лиссажу — [[парабола]] (''a''/''b'' = 2, ''δ'' = π/2). При других соотношениях фигуры Лиссажу представляют собой более сложные фигуры, которые являются замкнутыми при условии ''a''/''b'' — [[рациональное число]]. |
|||
Фигуры Лиссажу, где ''a'' = 1, ''b'' = ''N'' (''N'' — [[натуральное число]]) и |
|||
ИШ0и |
|||
: <math>\delta=\frac{N-1}{N}\frac{\pi}{2}\ </math> |
|||
Ш |
|||
являются [[Полиномы Чебышёва|полиномами Чебышёва]] первого рода степени ''N''.<!-- проверить перевод последней фразы of the first kind of degree ''N'' --> |
|||
== Примеры == |
|||
Анимация внизу показывает изменение кривых при постоянно возрастающем соотношении <math>\frac{a}{b}</math> от 0 до 1 с шагом 0.01. (δ=0) |
|||
[[Файл:Lissajous animation.gif|center]] |
|||
Примеры фигур Лиссажу ниже с ''δ'' = ''π''/2, нечётным [[натуральное число|натуральным числом]] ''a'', и также натуральным числом ''b'', и |''a'' − ''b''| = 1. |
|||
{{center|<gallery> |
|||
Image:Lissajous_curve_1by2.svg|{{center|''a'' = 1, ''b'' = 2 (1:2)}} |
|||
Image:Lissajous_curve_3by2.svg|{{center|''a'' = 3, ''b'' = 2 (3:2)}} |
|||
Image:Lissajous_curve_3by4.svg|{{center|''a'' = 3, ''b'' = 4 (3:4)}} |
|||
Image:Lissajous_curve_5by4.svg|{{center|''a'' = 5, ''b'' = 4 (5:4)}} |
|||
Image:Lissajous_curve_5by6.svg|{{center|''a'' = 5, ''b'' = 6 (5:6)}} |
|||
Image:Lissajous_curve_9by8.svg|{{center|''a'' = 9, ''b'' = 8 (9:8)}} |
|||
</gallery>}} |
|||
== Применение в технике — сравнение частот == |
|||
[[Файл:Lissajous figure scope 2.jpg|200px|thumb|Фигура Лиссажу на экране осциллографа]] |
|||
Если подать на входы «'''X'''» и «'''Y'''» [[Осциллограф|осциллографа]] сигналы близких частот, то на экране можно увидеть фигуры Лиссажу. Этот метод широко используется для сравнения частот двух источников сигналов и для подстройки одного источника под частоту другого. Когда частоты близки, но не равны друг другу, фигура на экране вращается, причем период цикла вращения является величиной, обратной разности частот, например, период оборота равен 2 с — разница в частотах сигналов равна 0,5 Гц. При равенстве частот фигура застывает неподвижно, в любой фазе, однако на практике, за счет кратковременных нестабильностей сигналов, фигура на экране осциллографа обычно чуть-чуть подрагивает. Использовать для сравнения можно не только одинаковые частоты, но и находящиеся в кратном отношении, например, если образцовый источник может выдавать частоту только 5 МГц, а настраиваемый источник — 2,5 МГц. |
|||
[[Файл:Lissajou rotating.gif|200px|thumb|Вращение фигуры Лиссажу при незначительной расстройке частот]] |
|||
== Литература == |
|||
* Справочник по радиоэлектронным устройствам. В 2-х томах; Под ред. Д. П. Линде — М.: Энергия, [[1978]] |
|||
* Справочник по физике. ''Яворский Б. М., Детлаф А. А.'' — М.: Наука, [[1981]] |
|||
== См. также == |
|||
* [[Колебания]] |
|||
* [[Частота периодического процесса]] |
|||
* [[Маятник Фуко]] |
|||
* [[Конические сечения]] |
|||
* [[Звезда (геометрия)#Другое определение|Связные звёзды]] |
|||
== Ссылки == |
|||
* [http://www.magnet.fsu.edu/education/tutorials/java/lissajous/index.html On-line построение фигур Лиссажу] |
|||
* [http://www.falstad.com/circuit/index.html Circuits. Over Passive Circuits. Lissajous Figures] |
|||
| ⚫ | |||
{{Кривые}} |
|||
Иш |
|||
{{rq|style}} |
|||
Щш |
|||
[[Категория:Теория колебаний]] |
[[Категория:Теория колебаний]] |
||
[[Категория:Методы измерений |
[[Категория:Методы измерений]] |
||
[[Категория:Кривые |
[[Категория:Кривые]] |
||
{{DEFAULTSORT:35452345234523}} |
|||
Версия от 11:24, 2 марта 2017
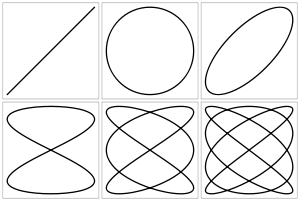
Фигу́ры Лиссажу́ — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёным Жюлем Антуаном Лиссажу. Вид фигур зависит от соотношения между периодами (частотами), фазами и амплитудами обоих колебаний. В простейшем случае равенства обоих периодов фигуры представляют собой эллипсы, которые при разности фаз 0 или вырождаются в отрезки прямых, а при разности фаз и равенстве амплитуд превращаются в окружность. Если периоды обоих колебаний неточно совпадают, то разность фаз всё время меняется, вследствие чего эллипс всё время деформируется. При существенно различных периодах фигуры Лиссажу не наблюдаются. Однако, если периоды относятся как целые числа, то через промежуток времени, равный наименьшему кратному обоих периодов, движущаяся точка снова возвращается в то же положение — получаются фигуры Лиссажу более сложной формы. Фигуры Лиссажу вписываются в прямоугольник, центр которого совпадает с началом координат, а стороны параллельны осям координат и расположены по обе стороны от них на расстояниях, равных амплитудам колебаний.
Математическое выражение для кривой Лиссажу
где A, B — амплитуды колебаний, a, b — частоты, δ — сдвиг фаз
Вид кривой сильно зависит от соотношения a/b. Когда соотношение равно 1, фигура Лиссажу имеет вид эллипса, при определённых условиях она имеет вид окружности (A = B, δ = π/2 радиан) и отрезка прямой (δ = 0). Ещё один пример фигуры Лиссажу — парабола (a/b = 2, δ = π/2). При других соотношениях фигуры Лиссажу представляют собой более сложные фигуры, которые являются замкнутыми при условии a/b — рациональное число.
Фигуры Лиссажу, где a = 1, b = N (N — натуральное число) и
являются полиномами Чебышёва первого рода степени N.
Примеры
Анимация внизу показывает изменение кривых при постоянно возрастающем соотношении от 0 до 1 с шагом 0.01. (δ=0)
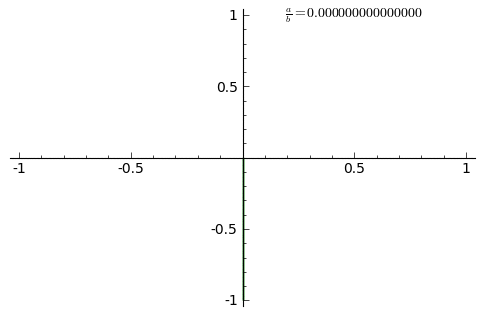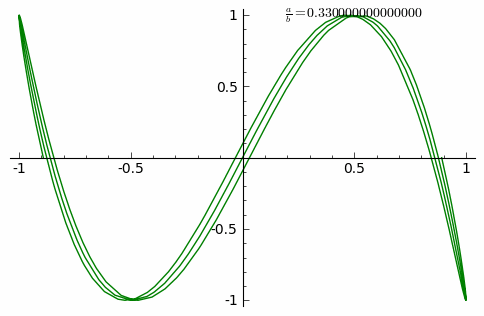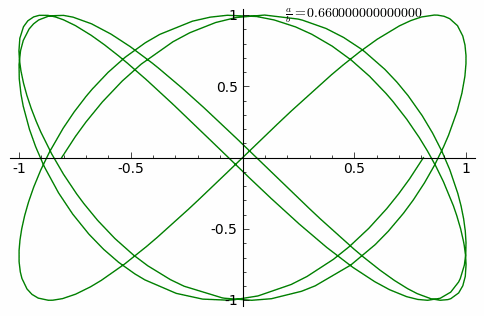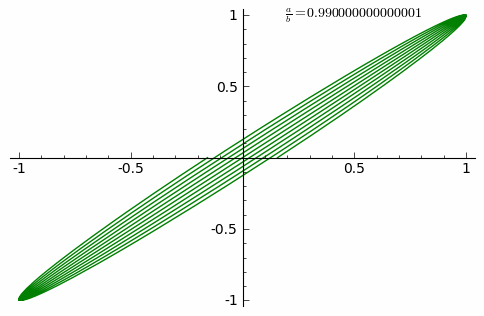
Примеры фигур Лиссажу ниже с δ = π/2, нечётным натуральным числом a, и также натуральным числом b, и |a − b| = 1.
-
a = 1, b = 2 (1:2)
-
a = 3, b = 2 (3:2)
-
a = 3, b = 4 (3:4)
-
a = 5, b = 4 (5:4)
-
a = 5, b = 6 (5:6)
-
a = 9, b = 8 (9:8)
Применение в технике — сравнение частот

Если подать на входы «X» и «Y» осциллографа сигналы близких частот, то на экране можно увидеть фигуры Лиссажу. Этот метод широко используется для сравнения частот двух источников сигналов и для подстройки одного источника под частоту другого. Когда частоты близки, но не равны друг другу, фигура на экране вращается, причем период цикла вращения является величиной, обратной разности частот, например, период оборота равен 2 с — разница в частотах сигналов равна 0,5 Гц. При равенстве частот фигура застывает неподвижно, в любой фазе, однако на практике, за счет кратковременных нестабильностей сигналов, фигура на экране осциллографа обычно чуть-чуть подрагивает. Использовать для сравнения можно не только одинаковые частоты, но и находящиеся в кратном отношении, например, если образцовый источник может выдавать частоту только 5 МГц, а настраиваемый источник — 2,5 МГц.
Литература
- Справочник по радиоэлектронным устройствам. В 2-х томах; Под ред. Д. П. Линде — М.: Энергия, 1978
- Справочник по физике. Яворский Б. М., Детлаф А. А. — М.: Наука, 1981
См. также
Ссылки
Для улучшения этой статьи желательно:
|










