Дифференциальная геометрия поверхностей: различия между версиями
| [отпатрулированная версия] | [отпатрулированная версия] |
Tosha (обсуждение | вклад) Нет описания правки |
Jumpow (обсуждение | вклад) Статья заменена переводом с английского статьи Differential geometry of surfaces |
||
| Строка 1: | Строка 1: | ||
[[Файл:Bendixen - Carl Friedrich Gauß, 1828.jpg|thumb|right|[[Гаусс, Карл Фридрих|Карл Фридрих Гаусс]] в 1828 году]] |
|||
[[Файл:Surface normal.png|thumb|right|The Gauss map sends a point on the surface to the outward pointing unit normal vector, a point on ''S''<sup>2</sup>]] |
|||
'''Дифференциальная геометрия поверхностей''' имеет дело с [[Дифференциальная геометрия и топология|дифференциальной геометрией]] [[Гладкое многообразие|гладких]] [[Поверхность|поверхностей]] с различными дополнительными структурами, наиболее часто, с [[Риманово многообразие|римановой метрикой]]. |
|||
Поверхности всесторонне изучались с различных точек зрения — ''внешней'', связанной с их [[вложение]]м в [[Евклидово пространство|евклидово пространство]], и ''внутренней'', отражающей свойства, определённые исключительно расстояниями внутри поверхности, полученными вдоль кривых на поверхности. Одной из исследованных фундаментальных концепций является [[Кривизна Гаусса|кривизна Гаусса]], впервые глубоко изучавшейся [[Гаусс, Карл Фридрих|Карлом Фридрихом Гауссом]]{{sfn|Gauss|1902}}, который показал, что кривизна является внутренним свойством поверхности, независящим от его изометричного вложения в евклидово пространство. |
|||
Поверхности естественным образом возникают как графики функций от пары переменных и иногда возникают в параметрической форме или как геометрические места точек, ассоциированные с [[Кривая|пространственными кривыми]]. Важную роль в их изучении играют [[Группа Ли|группы Ли]] (в духе [[Эрлангенская программа|эрлангенской программы]]), а именно группы симметрии евклидовой плоскости, сферы и гиперболической поверхности. Эти группы Ли могут быть использованы для описания поверхностей постоянной гауссовой кривизны. Они дают также существенный вклад в современные подходы к внутренней дифференциальной геометрии через [[Связность (дифференциальная геометрия)|связность]]. С другой стороны, внешние свойства, опирающиеся на вложение поверхности в евклидовом пространстве, также интенсивно изучались. Это хорошо иллюстрирует нелинейные [[Уравнение Эйлера — Лагранжа|уравнения Эйлера — Лагранжа]] в [[Вариационное исчисление|вариационном исчислении]] — хотя Эйлер рассматривал уравнения от одной переменной для понимания [[Геодезическая|геодезических]], определённых независимо от вложения, главные приложения уравнений от двух переменных были для [[Минимальная поверхность|минимальных поверхностей]], концепции, которую можно определить только в терминах вложения. |
|||
'''Дифференциальная геометрия поверхностей''' — раздел математики, изучающий [[поверхность|поверхности]] методами [[Дифференциальные геометрия и топология|дифференциальной геометрии]]. При этом исследуемые поверхности обычно подчинены условиям, связанным с возможностью применения методов [[Дифференциальное исчисление|дифференциального исчисления]]. Как правило, это — условия ''гладкости'' поверхности, то есть существования в каждой точке поверхности определённой [[Касательная прямая|касательной]] плоскости, кривизны и т. д. Эти требования сводятся к тому, что функции, задающие поверхность, предполагаются однократно, дважды, трижды, а в некоторых вопросах — неограниченное число раз [[дифференцируемая функция|дифференцируемыми]] или даже [[аналитическая функция|аналитическими функциями]]. При этом дополнительно накладывается условие регулярности. |
|||
== Обзор == |
|||
[[Многогранник]]и в [[Евклидово пространство|евклидовом пространстве]], такие как граница [[куб]]а, были среди первых поверхностей, с которыми встретилась геометрия. Можно также определить ''гладкие поверхности'', в которых каждая точка имеет окрестность, [[Диффеоморфизм|диффеоморфную]] некоторой открытой поверхности в <math>\mathbb{E}^2</math> [[Двумерное пространство|евклидовой плоскости]]. Это позволяет применять [[математический анализ]] к поверхностям для доказательства многих результатов. |
|||
Две гладкие поверхности диффеоморфны тогда и только тогда, когда они [[Гомеоморфизм|гомеоморфны]]. (Аналогичный результат не имеет место для многообразий размерности четыре и выше.) Отсюда следует, что [[Поверхность|замкнутые поверхности]] классифицируются с точностью до диффеоморфизма их [[Эйлерова характеристика|эйлеровой характеристикой]] и [[ориентируемость]]ю. |
|||
Гладкие поверхности, снабжённые [[Риманово многообразие|римановыми метриками]], имеют фундаментальную важность в дифференциальной геометрии. Риманова метрика снабжает поверхность понятиями [[Геодезическая|геодезической]], [[Расстояние|расстояния]], [[Угол|угла]] и площади. Важным классом таких поверхностей является [[Развёртывающаяся поверхность|развёртывающиеся поверхности]] — поверхности, которые могут быть расправлены в плоскость без растяжений. Примеры включают [[цилиндр]] и [[Коническая поверхность|конус]]. |
|||
Кроме того, есть свойства поверхностей, зависящие от вложения поверхности в евклидово пространство. Такие поверхности являются объектами рассмотрения внешней геометрии. К ним относятся |
|||
*[[Минимальная поверхность|Минимальные поверхности]], это поверхности, которые минимизируют площадь поверхности для заданных [[Краевая задача|краевых условий]]. Примеры включают [[Мыльный пузырь|мыльные плёнки]], натянутые на проволочную рамку, [[катеноид]]ы и [[геликоид]]ы. |
|||
*[[Линейчатая поверхность|Линейчатые поверхности]], это поверхности, которые имеют для каждой точки лежащую на поверхности по меньшей мере одну прямую, проходящую через эту точку. Примеры включают цилиндры и однолистные [[гиперболоид]]ы. |
|||
Любое {{math|''n''}}-мерное [[комплексное многообразие]] является, в то же время, {{math|2''n''}}-мерным вещественным многообразием. Тогда любой комплексный одно-многообразие (называемое также [[Риманова поверхность|римановой поверхностью]]) является гладкой ориентированной поверхностью с ассоциированной {{не переведено 5|Линейная комплексная структура|комплексной структурой||Linear complex structure}}. Любая замкнутая поверхность допускает комплексные структуры. Любая комплексная [[алгебраическая кривая]] или вещественная [[алгебраическая поверхность]] является также гладкой поверхностью, возможно, с сингулярностями. |
|||
Комплексные структуры на замкнутой ориентированной поверхности соответствуют {{не переведено 5|Конформная геометрия|классам комформной эквивалентности||conformally equivalent}} [[Риманово многообразие|римановых метрик]] на поверхности. Одна из версий {{не переведено 5|Теорема об униформации|теоремы об униформации||uniformization theorem}} (принадлежащая [[Пуанкаре, Анри|Пуанкаре]]) утверждает, что любая [[Риманово многообразие|риманова метрика]] на ориентированой замкнутой поверхности конформно эквивалентна по существу единственной метрике [[постоянная кривизна|постоянной кривизны]]. Это даёт отправную точку к одному из подходов к [[Пространство Тейхмюллера|теории Тейхмюллера]], которая обеспечивает более тонкую классификацию римановых поверхностей, чем топологическая классификация лишь по эйлеровой характеристике. |
|||
{{не переведено 5|Теорема об униформации|||uniformization theorem}} утверждает, что любая риманова поверхность {{math|''S''}} {{не переведено 5|Конформная геометрия|комформно эквивалентна||conformal equivalence}} поверхности, имеющей постоянную кривизну, которая может принимать значение 1, 0 или −1. Поверхность постоянной кривизны 1 локально [[Изометрия (математика)|изометрична]] сфере, что означает, что каждая точка поверхности имеет [[окрестность]], изометричную открытому множеству на единичной сфере в [[Евклидово пространство|<math>\mathbb{E}^3</math>]] с её внутренней римановой метрикой. Аналогично, поверхность постоянной кривизны 0 локально изометрична евклидовой плоскости, а поверхность постоянной кривизны −1 локально изометрична [[Геометрия Лобачевского|гиперболической плоскости]]. |
|||
[[Файл:Felix Klein.jpeg|thumb|right|upright|[[Клейн, Феликс|Феликс Клейн]] (1849-1925)]] |
|||
Поверхности постоянной кривизны являются двухмерными реализациями объектов, которые известны как [[Пространственная форма|пространственные формы]]. Они часто изучаются с точки зрения [[Эрлангенская программа|эрлангенской программы]] [[Клейн, Феликс|Феликса Клейна]] при помощи гладких [[Автоморфизм|групп автоморфизмов]]. Любая [[Связное пространство|связная]] поверхность с трёхмерной группой изометрий является поверхностью постоянной кривизны. |
|||
''Комплексная поверхность'' — это комплексное два-многообразие а потому, является вещественным четыре-многообразием. Это не поверхность в смысле этой статьи. |
|||
=== История поверхностей === |
|||
Отдельные свойства [[Поверхность вращения|поверхностей вращения]] были известны ещё [[Архимед]]у. Развитие [[Математический анализ|математического анализа]] в семнадцатом веке обеспечило более систематические подходы к их доказательству. Кривизну поверхностей общего виде первым изучал [[Эйлер, Леонард|Эйлер]]. В 1760 году{{sfn|Euler|1760}} он доказал формулу для кривизны поверхности, а в 1771 году{{sfn|Euler|1771}} он рассматривал поверхности, заданные в параметрической форме. [[Монж, Гаспар|Монж]] изложил основы его теории в классическом труде ''L'application de l'analyse à la géometrie'', который появился в 1795 году. Определяющий вклад в теорию поверхностей сделал [[Гаусс, Карл Фридрих|Гаусс]] в двух выдающихся статьях, написанных в 1825 и 1827 годах{{sfn|Gauss|1902}}. Они наметили новую линию, отличную от традиционной, поскольку впервые Гаусс рассматривал ''внутреннюю'' геометрию поверхности, свойства, которые определяются лишь геодезическими расстояниями между точками на поверхности независимо от способа, которым поверхность расположена в окружающем евклидовом пространстве. Завершающим результатом является [[Theorema Egregium]] Гаусса, устанавливающая, что [[кривизна Гаусса]] является внутренним инвариантом, то есть инвариантом относительно локальных [[Изометрия (математика)|изометрий]]. Эту точку зрения распространил на пространства высоких размерностей [[Риман, Бернхард|Риман]] и основал то, что сейчас называется [[Риманова геометрия|римановой геометрией]]. Девятнадцатый век был золотым веком теории поверхностей как с топологической, так и дифференциально-геометрической тoчки зрения, в котором многие ведущие геометры посвящали себя их изучению. [[Дарбу, Жан Гастон|Дарбу]] собрал много результатов в своём четырёхтомном трактате ''Théorie des surfaces'' (Теория поверхностей, 1887–1896). |
|||
Представленное ниже большей частью следует Гауссу, но с важными дополнениями от других геометров. В то время Гаусс был у [[Георг III|Георга III]] [[Картография|картографом]] Великобритании и [[Ганновер]]а. Это королевское покровительство может объяснить, почему эти работы содержат практические вычисления [[Форма Земли|кривизны земли]] чисто на основе измерений на поверхности планеты. |
|||
== Кривизна поверхности в евклидовом пространстве == |
|||
{{Основная статья|Кривизна}} |
|||
{{см. также|Евклидово пространство|Кривизна Гаусса|Средняя кривизна}} |
|||
[[Файл:Minimal surface curvature planes-en.svg|thumb|right|Главные кривизны в точке на поверхности]] |
|||
[[Файл:Surface normal.png|thumb|right|Отображение Гаусса точки на поверхности в направленный наружу единичный нормальный вектор, точку на <math>S^2</math>]] |
|||
Неформально Гаусс определяет кривизну поверхности в терминах кривизны некоторых плоских кривых, связанных с поверхностью. Он позднее нашёл серию эквивалентных определений. Одно из первых было сформулировано в терминах свойств отображения Гаусса, отображения из поверхности в 2-мерную сферу. Однако, до получения более естественного определения в терминах площади углов малых треугольников, Гауссу потребовалось осуществить глубокое исследование свойств геодезической на поверхности, то есть путей кратчайшей длины между двумя фиксированными точками на поверхности (см. ниже).{{efn|1=Это конечное положение резинки, натянутой между двумя фиксированными точками на поверхности.}} |
|||
'''Гауссова кривизна''' в точке на вложенной гладкой поверхности, заданной локально уравнением |
|||
: <math>z = F(x,y)</math> |
|||
в евклидовом пространстве (<math>\mathbb{E}^3</math>), определяется как произведение [[Главная кривизна|главных кривизн]] в точке{{sfn|Berger|2004}}. '''Средняя кривизна''' определяется как их среднее. Главные кривизны — это максимальная и минимальная [[Кривизна|кривизны]] [[Плоская кривая|плоских кривых]], полученных путём пересечения поверхности с плоскостями, перпендикулярными касательной плоскости в точке. Если точкой является {{math|(0, 0, 0)}} с касательной плоскостью <math>z = 0</math>, то, после вращения вокруг оси {{math|''z''}} и обнуления коэффициента при {{math|''xy''}}, {{math|''F''}} будет иметь разложение в ряд Тейлора |
|||
:<math>F(x, y) = \tfrac{1}{2} k_1 x^2 + \tfrac{1}{2} k_2 y^2 + \cdot\cdot\cdot</math> |
|||
Главными кривизнами являются <math>k_1</math> и <math>k_2</math>. В этом случае гауссова кривизна задаётся формулой |
|||
:<math>K=k_1\cdot k_2.</math> |
|||
а средняя кривизна формулой |
|||
:<math>K_m=\tfrac{1}{2} (k_1 + k_2).</math> |
|||
Поскольку <math>K</math> и <math>K_m</math> являются инвариантами относительно [[Изометрия (математика)|изометрий]] <math>\mathbb{E}^3</math>, в общем случае |
|||
:<math>K = \frac{RT - S^2}{\left( 1 + P^2 + Q^2 \right)^2}</math> |
|||
и |
|||
:<math>K_m =\frac{ET + GR - 2FS}{2\left(1 + P^2 + Q^2\right)^2}</math> |
|||
где производные в точке вычисляются по формулам{{sfn|Eisenhart|2004|с=123}} |
|||
<math>P=F_x,Q=F_y,R=F_{xx},S=F_{xy},T=F_{yy}</math> |
|||
<math>E=1+F_x^2,G=1+F_y^2,F=F_xF_y</math> |
|||
Для любой ориентированной вложенной поверхности '''[[отображение Гаусса]]''' является отображением в единичную сферу, отображающим каждую точку в (направленный наружу) единичный [[Нормаль|нормальный вектор]] к ориентированной касательной плоскости в точке. В системе координат отображение отображает точку <math>(x,y,z)</math> в |
|||
:<math>N(x, y, z) = \frac{1}{\sqrt{1 + P^2 + Q^2}} (P, Q, -1).</math> |
|||
Прямые вычисления показывают, что ''гауссова кривизна является [[Матрица Якоби|якобианом]] отображения Гаусса''{{sfn|Singer, Thorpe|1967|с=223}}. |
|||
== Примеры == |
|||
[[Файл:Surface of revolution illustration.png|thumb|right|Поверхность вращения, полученная путём вращения кривой <math>x = 2 + \cos z</math> вокруг оси {{math|''z''}}.]] |
|||
=== Поверхности вращения === |
|||
{{Подробная статья|Поверхность вращения}} |
|||
Поверхность вращения может быть получена вращением кривой в плоскости {{math|''xz''}} вокруг оси {{math|''z''}} в предположении, что кривая не пересекает ось {{math|''z''}}. Предположим, что кривая задана выражением |
|||
:<math> x= \varphi(t),\,\, z=\psi(t)</math> |
|||
с {{math|''t''}} лежащим в {{math|(''a'', ''b'')}}, и параметризованная длиной дуги, так что |
|||
:<math> \dot{\varphi}^2 + \dot{\psi}^2 = 1.</math> |
|||
Тогда поверхность вращения является множеством точек |
|||
:<math>M=\{(\varphi(t)\cos \theta, \varphi(t)\sin \theta,\psi(t))\colon t\in (a,b), \theta\in [0,2\pi)\}.</math> |
|||
Гауссова кривизна и средняя кривизна задаются выражениями{{sfn|do Carmo|1976|с=161–162}} |
|||
:<math> K = -{\ddot{\varphi}\over \varphi},\,\, K_m = {-\dot{\psi} +\varphi(\dot{\psi}\ddot{\varphi} -\ddot{\psi}\dot{\varphi})\over 2 \varphi}. </math> |
|||
[[Файл:Ellipsoid Quadric.png|thumb|right|[[Эллипсоид]], поверхность второго порядка]] |
|||
Геодезические на поверхности вращение определяются {{не переведено 5|Отношение Клеро|отношением Клеро||Clairaut's relation}}. |
|||
=== Поверхность второго порядка === |
|||
{{Подробная статья|Поверхность второго порядка}} |
|||
Рассмотрим поверхность второго порядка, заданную выражением{{sfn|Eisenhart|2004|с=228–229}} |
|||
:<math> {x^2\over a} + {y^2\over b} +{z^2\over c}=1.</math> |
|||
Эта поверхность позволяет параметризацию |
|||
:<math>x=\sqrt{a(a-u)(a-v)\over (a-b)(a-c)},\,\, y=\sqrt{b(b-u)(b-v)\over (b-a) (b-c)}, \,\, z=\sqrt{c(c-u)(c-v)\over (c-b)(c-a)}.</math> |
|||
Гауссова кривизна и средняя кривизна задаются выражением |
|||
:<math>K={abc\over u^2 v^2} ,\,\,K_m=-(u+v)\sqrt{abc\over u^3v^3}.</math> |
|||
[[Файл:Ruled hyperboloid.jpg|thumb|right|Однолистный [[гиперболоид]], являющийся линейчатой поверхностью в двух различных направлениях.]] |
|||
=== Линейчатые поверхности === |
|||
{{Подробная статья|Линейчатая поверхность}} |
|||
Линейчатая поверхность является поверхностью, которая может быть получена движением прямой линии в <math>\mathbb{E}^3</math>{{sfn|Eisenhart|2004|с=241–250}}{{sfn|do Carmo|1976|с=188–197}}. Выбрав ''директрису'' на поверхности, то есть гладкую кривую единичной скорости {{math|''c''(''t'')}}, ортогональную прямым, а затем выбрав <math>u(t)</math> как единичные вектора вдоль кривой в направлении прямых, для вектора скорости <math>v = c_t</math> и {{math|''u''}} выполняется |
|||
:<math>u\cdot v=0, \,\,\|u\|=1,\,\,\|v\|=1.</math> |
|||
Поверхность состоит из точек |
|||
:<math>c(t) + s\cdot u(t)</math> |
|||
при изменении {{math|''s''}} и {{math|''t''}}. |
|||
Тогда, если |
|||
:<math>a=\|u_t\|, \,\, b=u_t\cdot v, \,\, \alpha=-\frac{b}{a^2}, \,\, \beta=\frac{\sqrt{a^2-b^2}}{a^2},</math> |
|||
гауссова и средняя кривизна задаются выражениями |
|||
:<math>K=-{\beta^2\over ((s-\alpha)^2 +\beta^2)^2} ,\,\, K_m=-{r[(s-\alpha)^2 +\beta^2)] +\beta_t(s-\alpha) + \beta\alpha_t\over |
|||
[(s-\alpha)^2 +\beta^2]^{\frac32}}.</math> |
|||
Гауссова кривизна линейчатой поверхности обращается в нуль тогда и только тогда, когда <math>u_t</math> и {{math|''v''}} пропорциональны{{sfn|do Carmo|1976|с=194}}. Это условие эквивалентно тому, что поверхность является [[Огибающая|огибающей]] плоскостей вдоль кривой, содержащей касательный вектор {{math|''v''}} и ортогональный вектор {{math|''u''}}, то есть поверхность является [[Развёртывающаяся поверхность|развёртывающейся]] вдоль кривой{{sfn|Eisenhart|2004|с=61–65}}. Более обще поверхность в <math>\mathbb{E}^3</math> имеет нулевую гауссову кривизну близ точки тогда и только тогда, когда она развёртывается вблизи этой точки{{sfn|Eisenhart|2004}} (Эквивалентное условие даётся ниже в терминах метрики.) |
|||
=== Минимальные поверхности === |
|||
{{Подробная статья|Минимальная поверхность}} |
|||
В 1760 году [[Лагранж, Жозеф Луи|Лагранж]] распространил результаты Эйлера [[Вариационное исчисление|вариационного исчисление]] с интегралами от одной переменной на интегралы от двух переменных{{sfn|Eisenhart|2004|с=250–269}}{{sfn|do Carmo|1976|с=197–213}}. Он обдумывал следующую задачу: |
|||
{{quotation|Если дана замкнутая кривая в <math>\mathbb{E}^3</math>, находим поверхность минимальной площади, имеющая кривую в качестве границы.}} |
|||
Такая поверхность называется '''минимальной поверхностью'''. |
|||
В 1776 году [[Мёнье де ла Плас, Жан Батист|Жан Батист Мёнье]] показал, что дифференциальное уравнение, полученное Лагранжем, эквивалентно обращению в нуль средней кривизны поверхности: |
|||
{{quotation|Поверхность минимальна тогда и только тогда, когда средняя кривизна обращается в нуль.}} |
|||
Минимальные поверхности имеют простую интерпретацию в реальной жизни — они имеют форму мыльной плёнки, если проволочную рамку окунуть в мыльный раствор и осторожно вынуть. Вопрос, существует ли минимальная поверхность с заданной границей, называется [[Задача Плато|задачей Плато]] по имени бельгийского физика [[Плато, Жозеф|Жозефа Плато]], который проводил эксперименты с мыльными плёнками в середине девятнадцатого века. В 1930 году [[Дуглас, Джесси|Джесси Дуглас]] и Тибор Радо дали положительный ответ на задачу Плато (Дуглас получил одну из первых [[Филдсовская премия|филдсовских премий]] за эту работу в 1936 году)<ref>Решение Дугласа описано в статье Куранта ({{harv|Courant|1950}}).</ref>. |
|||
Известно много примеров минимальных поверхностей, такие как [[катеноид]], [[геликоид]], {{не переведено 5|поверхность Шерка|||Scherk surface}} и [[поверхность Эннепера]]. В этой области проводились интенсивные исследования, итог которых подведён в книге Оссермана{{sfn|Osserman|2002}}. В частности, результат Оссермана показывает, что если минимальная поверхность не планарна, то её образ при отображении Гаусса плотен в <math>S^2</math>. |
|||
[[Файл:Gaussian curvature.svg|thumb|right|Поверхности с постоянной отрицательной, нулевой и положительной кривизной Гаусса]] |
|||
=== Поверхности постоянной гауссовой кривизны === |
|||
[[Файл:Beltrami.jpg|thumb|right|upright|[[Бельтрами, Эудженио|Эудженио Бельтрами]] (1835-1899)]] |
|||
Если поверхность имеет постоянную гауссову кривизну, она называется '''поверхностью постоянной кривизны'''{{sfn|Eisenhart|2004|с=270–291}}{{sfn|O'Neill|1997|с=249–251}}{{sfn|Hilbert, Cohn-Vossen|1952}}. |
|||
*Единичная [[сфера]] в <math>\mathbb{E}^3</math> имеет постоянную гауссову кривизну +1. |
|||
*Евклидова [[плоскость]] и [[цилиндр]] имеют постоянную гауссову кривизну 0. |
|||
*Поверхность вращения с <math>\varphi_{tt} = \varphi</math> имеет постоянную гауссову кривизну –1. Частный случай получается путём принятия <math>\varphi(t) = C \mathrm{ch}\,t</math>, <math>C \mathrm{sh}\,t</math> и <math>C e^t</math>{{sfn|O'Neill|1997|с=249–251}}{{sfn|do Carmo|1976|с=168–170}}{{sfn|Gray, Abbena, Salamon|2006}}. Последний случай является классической [[псевдосфера|псевдосферой]], образованной вращением [[Трактриса|трактрисы]] вокруг центральной оси. В 1868 году [[Бельтрами, Эудженио|Эудженио Бельтрами]] показал, что геометрия псеводосферы была напрямую связана с геометрией [[Геометрия Лобачевского|гиперболической плоскости]], открытой независимо [[Лобачевский, Николай Иванович|Лобачевским]] (1830) и [[Бойяи, Янош|Бойяи]] (1832). Уже в 1840 году Ф. Майндинг, студент Гаусса, получил тригонометрические формулы для псевдосферы, идентичные формулам для гиперболической плоскости{{sfn|Stillwell|1996|с=1–5}}. Эта поверхность постоянной кривизны ныне лучше понимается в терминах [[Метрика Пуанкаре|метрики Пуанкаре]] на [[Верхняя полуплоскость|верхней полуплоскости]] или [[Единичный круг|единичном круге]] и может быть описана другими моделями, такими как [[Проективная модель|модель Кляйна]] или [[гиперболоидная модель]], полученная рассмотрением двулистного гиперболоида <math>q(x, y, z) = -1</math> в трёхмерном [[Пространство Минковского|пространстве Минковского]], где <math>q(x, y, z) = x^2 + y^2 - z^2</math>{{sfn|Wilson|2008}}. |
|||
Каждая из этих поверхностей постоянной кривизны имеет [[Действие группы|транзитивную]] [[Группа Ли|группу Ли]] симметрий. Этот теоретико-групповой факт имеет далеко идущие следствия, которые особенно замечательны ввиду центральной роли, которую играют эти специальные поверхности в геометрии поверхностей согласно {{не переведено 5|Теорема об униформации|теореме об униформации||uniformization theorem}} [[Пуанкаре, Анри|Пуанкаре]] (см. ниже). |
|||
Другие примеры поверхностей с гауссовой кривизной 0 включают [[конус]]ы, |
|||
{{не переведено 5|Развёртывающаяся поверхность касательных|развёртывающиеся поверхности касательных||tangent developable}} и, более обще, любая [[развёртывающаяся поверхность]]. |
|||
== Структура локальной метрики == |
|||
{{Подробная статья|Риманово многообразие}} |
|||
[[Файл:Sphere with chart.svg|thumb|right|upright|Карта для верхней полусферы, полученная проекцией на плоскость {{math|''xy''}}]] |
|||
[[Файл:Transition functions in an atlas.svg|thumb|right|Изменения координат между двумя различными картами должны быть гладкими]] |
|||
Для любой поверхности, вложенной в евклидово пространство размерности 3 и выше, можно измерить длину кривой на поверхности, угол между двумя кривыми и площадь области на поверхности. Эта структура закодирована инфинитезимально в '''[[Риманово многообразие|римановой метрике]]''' на поверхности через ''элементы линий'' и ''элементы площади''. В девятнадцатом и в начале двадцатого века рассматривались только поверхности, вложенные в <math>\mathbb{R}^3</math>, а метрика задавалась как 2×2 [[положительно определённая матрица]], гладко меняющаяся от точки к точке в локальной параметризации поверхности. Идея локальной параметризации и изменение координат были формализованы позднее через абстрактное понятие [[Многообразие|многообразия]], топологического пространства, где {{не переведено 5|гладкая структура|||smooth structure}} задана локальными картами на многообразии, в точности как планета Земля отображается [[Географический атлас|атласами]] сегодня. Изменения координат между различными картами той же самой области должны быть гладкими. Как контурные линии в реальных картах кодируют изменения в высоте над уровнем моря, принимая во внимание локальные искажения земной поверхности при вычислении истинных расстояний, так и риманова метрика описывает расстояния и площади «в малом» в каждой локальной карте. В каждой локальной карте риманова метрика задаётся гладко 2×2 положительно определённой матрицей в каждой точке. Когда берутся различные карты, матрица преобразуется согласно [[Матрица Якоби|матрице Якоби]] изменения координат. Многообразие тогда имеет структуру 2-мерного [[Риманово многообразие|риманового многообразия]]. |
|||
=== Элементы линии и площади === |
|||
При выборе локальной карты, например, путём проекции на плоскость <math>xy (z = 0)</math>, элемент линии {{math|''ds''}} и элемент площади {{math|''dA''}} могут быть записаны в терминах локальных координат |
|||
:<math>ds^2 = E dx^2 + 2F dx dy + G dy^2</math> |
|||
и |
|||
:<math>dA = (EG - F^2)^{\tfrac{1}{2}} dx dy</math>. |
|||
Выражение <math>E dx^2 + 2F dx dy + G dy^2</math> называется '''первой фундаментальной формой'''{{sfn|Levi-Civita|1917}}. |
|||
Матрица |
|||
:<math>\begin{pmatrix} |
|||
E(x,y) & F(x,y) \\ |
|||
F(x,y) & G(x,y)\end{pmatrix}</math> |
|||
должна быть [[Положительно определённая матрица|положительна определена]] и гладко зависит от {{math|''x''}} и {{math|''y''}}. |
|||
Аналогичным образом элементы линии и площади могут быть ассоциированы с любым абстрактным [[Риманово многообразие|римановом 2-многообразии]] в локальном графике. |
|||
=== Вторая фундаментальная форма === |
|||
{{Основная статья|Вторая фундаментальная форма}} |
|||
[[Файл:Second fundamental form.svg|thumb|right|Определение второй фундаментальной формы]] |
|||
Внешняя геометрия поверхностей изучает свойства поверхностей, вложенных в евклидово пространство, обычно <math>\mathbb{E}^3</math>. Во внутренней геометрии две поверхности «одинаковы», если можно разогнуть одну поверхность в другую без растяжений, то есть образовать отображение одной поверхности в другую с сохранением расстояния. Так, цилиндр локально «одинаков» с плоскостью. Во внешней геометрии две поверхности «одинаковы», если они [[Конгруэнтность (геометрия)|конгруэнтны]] в объемлющем евклидовом пространстве, то есть существует [[Изометрия (математика)|изометрия]] <math>\mathbb{E}^3</math>, переводящая одну поверхность в другую. С этим более жёстким определением одинаковости цилиндр и плоскость, очевидно, уже не одинаковы. |
|||
Хотя главными инвариантами при изучении внутренней геометрии поверхности являются метрика (первая фундаментальная форма) и гауссова кривизна, некоторые свойства поверхностей зависят также от вложения в <math>\mathbb{E}^3</math> (или в евклидово пространство большей размерности). Наиболее важным примером является '''вторая фундаментальная форма''', которая классически определяется следующим образом{{sfn|Eisenhart|2004|с=114–115}}{{sfn|Pressley|2001|с=123–124}}{{sfn|Wilson|2008|с=123–124}}. |
|||
Возьмём точку <math>(x, y)</math> на поверхности в [[Атлас (топология)|локальной карте]]. Евклидово расстояние от близкой точки <math>(x + dx, y + dy)</math> до касательной плоскости в (''x'', ''y''), то есть длина перпендикуляра, опущенного из этой точки на касательную плоскость имеет вид |
|||
:<math>e dx^2 + 2f dx dy + g dy^2</math> |
|||
плюс третья и более высокие поправки. Выражение выше, симметричная билинейная форма в каждой точке, является второй фундаментальной формой. Она описывается <math>2 \times 2</math> [[Симметричная матрица|симметричной матрицей]] |
|||
:<math>\begin{pmatrix} |
|||
e(x,y) & f(x,y) \\ |
|||
f(x,y) & g(x,y)\end{pmatrix}</math> |
|||
которая зависит гладко от {{math|''x''}} и {{math|''y''}}. Гауссову кривизну можно вычислить как отношение определителей второй и третьей фундаментальаных форм: |
|||
:<math>K={eg-f^2\over EG-F^2}</math> |
|||
Следует заметить, что Гаусс доказал, что она является внутренним инвариантом (см. его Theorema Egregium ниже). |
|||
Одним из других внешних численных инвариантов поверхности является '''[[средняя кривизна|средняя кривизна]]''' <math>K_m</math>, определённая как ''сумма'' главных кривизн. Она задаётся формулой{{sfn|Levi-Civita|1917}} |
|||
:<math>K_m={1 \over 2} \cdot {eG + gE - 2 fF\over EG -F^2}</math> |
|||
Коэффициенты первой и второй фундаментальных форм удовлетворяют определённым условиям совместимости, известным как [[Уравнения Петерсона ― Кодацци|уравнения Гаусса ― Кодацци]]. Они используют [[символы Кристоффеля]] <math>\Gamma_{ij}^k</math>, связанные с первой фундаментальной формой{{sfn|Eisenhart|2004|с=156}}: |
|||
:<math>e_y-f_x=e\Gamma_{12}^1 + f(\Gamma_{12}^2-\Gamma_{11}^1) - g\Gamma_{11}^2</math> |
|||
:<math>f_y-g_x=e\Gamma_{22}^1 + f(\Gamma_{22}^2-\Gamma_{12}^1) - g\Gamma_{12}^2.</math> |
|||
Эти равенства могут также быть {{не переведено 5|Риманова связность на поверхности| кратко выражены и выведены||Riemannian connection on a surface}} на языке [[Форма связности|форм связности]] (согласно [[Картан, Эли Жозеф|Эли Картану]]{{sfn|O'Neill|1997|с=257}}). [[Бонне, Пьер Оссиан|Пьер Бонне]] доказал, что две квадратичные формы, удовлетворяющие уравнениям Гаусса — Годацци, всегда однозначно определяют вложенную поверхность локально{{sfn|do Carmo|1976|с=309–314}}. По этой причине уравнения Гаусса — Кодацци часто называют фундаментальными уравнениями для вложенных поверхностей, они точно определяют, откуда пришла внутренняя и внешняя кривизны. Они позволяют обобщения на поверхности, вложенные в более общие [[Риманово многообразие|римановы многообразия]]. |
|||
=== Оператор формы === |
|||
[[Файл:Wilhelm Blaschke.jpg|thumb|right|upright|Вильгельм Бляшке (1885-1962)]] |
|||
[[Дифференциал (математика)|Дифференциал]] {{math|''df''}} [[Отображение Гаусса|отображения Гаусса]] {{math|''f''}} может быть использован для определения типа внешней кривизны, известной как '''оператор формы'''{{sfn|O'Neill|1997|с=195–216}}{{sfn|do Carmo|1976|с=134–153}}{{sfn|Singer, Thorpe|1967|с=216–224}} или отображение Вейнгартена. Этот оператор первый раз появился явно в работе [[Бляшке, Вильгельм|Вильгельма Бляшке]] и позднее явно в трактате Бурали-Форти и Бугатти{{sfn|Gray, Abbena, Salamon|2006|с=386}}. Поскольку в каждой точке {{math|''x''}} поверхности касательное пространство является [[Предгильбертово пространство|пространством со скалярным произведением]], оператор формы <math>S_x</math> можно определить как линейный оператор на этом пространстве фомйлой |
|||
:<math> (S_x v, w) =(df(v), w)</math> |
|||
для касательных векторов {{math|''v''}}, {{math|''w''}} (скалярное произведение имеет смысл, поскольку <math>df(v)</math> и {{math|''w''}} оба лежат в <math>\mathbb{E}^3</math>){{efn|1=Заметим, что в некоторых более свежих текстах симметричная билинейная форма в правой части называется второй фундаментальной формой, однако это не соответствует классическому определению второй фундаментальной формы.}}. Правая часть симметрична по {{math|''v''}} и {{math|''w''}}, так что оператор формы является [[Симметричная матрица|самосопряжённым]] на касательном пространстве. Собственные значения <math>S_x</math> являются главными кривизнами <math>k_1</math> и <math>k_2</math> в {{math|''x''}}. В частности, [[определитель]] оператора формы в точке является гуссовой кривизной, но он содержит также другую информацию, поскольку [[средняя кривизна]] является половиной [[След матрицы|следа]] оператора формы. Средняя кривизна является внешним инвариантом. Во внешней геометрии цилиндр является развёртывающимся, что означает, что любая часть его внутренне неразличима от части плоскости, поскольку его кривизна Гаусса одинаково обращается в нуль. Хотя, его средняя кривизна не равна нулю. Следовательно, внешне он отличается от плоскости. |
|||
В общем случае [[Собственный вектор|собственные вектора и значения]] оператора формы в каждой точке определяют направления, в которых поверхность изгибается в каждой точке. Собственные значения соответствуют [[Главная кривизна|главным кривизнам]] поверхности, а собственные вектора соответствуют главным направлениям. Главные направления задают направления, в которых вложенная в поверхность кривая должна идти, чтобы максимизировать или минимизировать кривизну. |
|||
Оператор формы задаётся в терминах компонент первой и второй фундаментальных форм {{не переведено 5|уравнение Вейнгартена|уравнением Вейнгартена||Weingarten equations}}{{sfn|Gray, Abbena, Salamon|2006|с=394}}: |
|||
:<math>S= (EG-F^2)^{-1}\begin{pmatrix} |
|||
eG-fF& fG-gF \\ |
|||
fE-eF & gE- fF\end{pmatrix}.</math> |
|||
== Геодезические кривые на поверхности == |
|||
Кривые на поверхности, которые имею минимальную длину между двумя точками, называются [[геодезическая|геодезическими]]. Это формы, которые принимает [[Канцелярская резинка|резинка]], натянутая между двумя точками. Математически геодезические описываются с помощью [[Дифференциальное уравнение в частных производных|дифференциального уравнения в частных производных]] из [[Вариационное исчисление|вариационного исчисления]]. Дифференциальная геометрия поверхностей вращается вокруг изучения геодезических. Остаётся открытым вопрос, любая ли риманова метрика на 2-мерной локальной карте возникает из вложения в 3-мерное евклидово пространство — теория геодезических обычно указывает, что это верно в важном случае, когда компоненты метрики являются [[Аналитическая функция|аналитическими]]. |
|||
=== Геодезические === |
|||
[[Файл:Spherical triangle.svg|thumb|right|upright|Геодезический треугольник на сфере. |
|||
Геодезические являются дугами [[Большой круг|большого круга]].]] |
|||
Если имеется кусочно гладкий путь <math>c(t) = (x(t), y(t))</math> в карте для {{math|''t''}} на {{math|[''a'', ''b'']}}, его ''длина'' определяется выражением |
|||
:<math> L(c) = \int_a^b (E\dot{x}^2 + 2F \dot{x}\dot{y} + G \dot{y}^2)^{\frac12}\, dt </math> |
|||
а ''энергия'' выражением |
|||
:<math> E(c) = \int_a^b (E\dot{x}^2 + 2F \dot{x}\dot{y} + G \dot{y}^2)\, dt. </math> |
|||
Длина не зависит от параметризации пути. Согласно [[Уравнение Эйлера — Лагранжа|уравнениям Эйлера — Лагранжа]], если <math>c(t)</math> является путём, минимизирующим длину и ''параметризированным длиной дуги'', он должен удовлетворять [[Список объектов, названных в честь Леонарда Эйлера|уравнениям Эйлера]] |
|||
:<math>\ddot{x} + \Gamma_{11}^1 \dot{x}^2 + 2\Gamma_{12}^1 \dot{x}\dot{y}+ \Gamma_{22}^1\dot{y}^2 =0</math> |
|||
:<math>\ddot{y}+ \Gamma_{11}^2 \dot{x}^2 + 2\Gamma_{12}^2 \dot{x}\dot{y}+ \Gamma_{22}^2 \dot{y}^2 =0</math> |
|||
где [[символы Кристоффеля]] <math>\Gamma_{ij}^k </math> задаются выражением |
|||
:<math>\Gamma_{ij}^k = \tfrac12 \sum_m g^{km} (\partial_j g_{im} + \partial_i g_{jm} - \partial_m g_{ij})</math> |
|||
где <math>g_{11} = E, g_{12} = F, g_{22} = G</math> и <math>g_{ij}</math> является матрицей, обратной <math>g_{ij}</math>. Путь, удовлетворяющий уравнениям Эйлера, называется '''[[Геодезическая|геодезической]]'''. Согласно [[Неравенство Коши — Буняковского|неравенству Коши — Буняковского]] минимизирующий энергию путь — это просто геодезическая, параметризованая длиной дуги, и для любой геодезической параметр {{math|''t''}} пропорционален длине дуги{{sfn|Berger|2004}}{{sfn|Wilson|2008}}{{sfn|Milnor|1963}}. |
|||
=== Геодезическая кривизна === |
|||
{{см. также|Геодезическая кривизна|Поверхность Дарбу}} |
|||
'''Геодезическая кривизна''' <math>k_g</math> в точке кривой <math>c(t)</math>, параметризованная длиной дуги, на ориентированной поверхности определяется выражением{{sfn|Eisenhart|2002|с=131}}{{sfn|Berger|2004|с=39}}{{sfn|do Carmo|1976|с=248}}{{sfn|O'Neill|1997|с=237}} |
|||
:<math>k_g= \ddot{c}(t)\cdot \mathbf{n}(t).</math> |
|||
где <math> \mathbf{n}(t)</math> является «главной» единичной нормалью к кривой на поверхности, построенной путём вращения единичного касательного вектора <math>\mathbf{\dot c}(t)</math> на угол +90°. |
|||
*Геодезическая кривизна в точке является внутренним инвариантом, зависящим только от метрики близ точки. |
|||
*Кривая единичной скорости на поверхности является геодезической тогда и только тогда, когда её геодезическая кривизна принимает значение нуль во всех точках на кривой. |
|||
* Кривая единичной скорости <math>c(t)</math> во вложенной поверхности является геодезической тогда и только тогда, когда её вектор ускорения <math>\mathbf{\ddot c}(t)</math> нормален к поверхности. |
|||
Геодезическая кривизна измеряет точным образом как далека кривая на поверхности от геодезической. |
|||
=== Задача изометричного вложения === |
|||
Результат Якобовича{{sfn|Jacobowitz|1972}} и Позняка{{sfn|Poznjak|1973}} показывает, что любая метрическая структура на поверхности возникает из локального вложения в <math>\mathbb{E}^4</math>. Помимо некоторых специальных случаев остаётся открытым вопрос, возможно ли это в <math>\mathbb{E}^3</math>, так называемая «проблема Вейля»{{sfn|Han, Hong|2006}}. В 1926 году Морис Жане доказал, что это всегда возможно локально, если {{math|''E''}}, {{math|''F''}} и {{math|''G''}} [[Аналитическая функция|аналитичны]]. Вскоре после этого [[Картан, Эли Жозеф|Эли Картан]] обобщил это на локальные вложения [[Риманово многообразие|римановых {{math|''n''}}-многообразий]] в <math>\mathbb{E}^m</math>, где <math>m = \tfrac{n^2 + n}{2}</math>. Для доказательства теоремы Жане вблизи (0,0), [[теорема Коши — Ковалевской]] используется дважды для получения аналитических геодезических ортогональных оси {{math|''y''}}, а затем {{math|''x''}}, чтобы сделать аналитические изменения координат так, что <math>E = 1</math> и <math>F = 0</math>. [[Вложение|Изометрическое вложение]] {{math|''u''}} должно удовлетворять |
|||
:<math>u_x \cdot u_x = 1, u_x \cdot u_y = 0, u_y \cdot u_y = G</math>. |
|||
Дифференцирование даёт три дополнительных равенства |
|||
:<math>u_{xx} \cdot u_y = 0, u_{xx} \cdot u_x = 0, u_{xx} \cdot u_{yy} = u_{xy} \cdot u_{xy} - \tfrac{1}{2}G_{xx}</math>. |
|||
с заданными <math>u(0,y)</math> и <math>u_x(0,y)</math>. Эти уравнения можно решить около (0,0) с помощью теоремы Коши — Ковалевской и получить решение исходных уравнений вложения. |
|||
[[Файл:Tangency Example 2.svg|thumb|right|В ортогональной системе координат <math>\varphi</math> являет углом, который касательная {{math|''L''}} к геодезической {{math|''C''}} образует с осью {{math|''x''}}]] |
|||
=== Ортогональные координаты === |
|||
Когда <math>F = 0</math> в метрике, прямые, параллельные осям {{math|''x''}} и {{math|''y''}}, [[Ортогональность|ортогональны]] и дают '''[[Ортогональная система координат|ортогональные координаты]]'''. Если <math>H = (EG)^{\tfrac{1}{2}}</math>, то гауссова кривизна задаётся выражением{{sfn|Eisenhart|2004}}{{sfn|Taylor|1996a|с=Appendix C}}. |
|||
:<math> K=-{1\over 2H} \left[\partial_x\left(\frac{G_x}{H}\right) +\partial_y\left(\frac{E_y}{H}\right)\right].</math> |
|||
Если вдобавок <math>E = 1</math>, так что <math>H = G^{\tfrac{1}{2}}</math>, то угол <math>\varphi</math> в точке пересечения между геодезической <math>(x(t),y(t))</math> и прямой {{math|''y''}} = constant задаётся уравнениением |
|||
:<math>\tg \varphi = H\cdot \frac{\dot{y}}{\dot{x}}.</math> |
|||
Производная <math>\varphi</math> задаётся классической формулой Гаусса{{sfn|Eisenhart|2004}}{{sfn|Berger|2004}}: |
|||
:<math> \dot{\varphi} = -H_x \cdot \dot{y}.</math> |
|||
== Геодезические полярные координаты == |
|||
[[Файл:Carl Jacobi.jpg|thumb|right|[[Якоби, Карл Густав Якоб|Карл Якоби]] (1804–1851)]] |
|||
[[Файл:GaussJacobi.jpg|thumb|right|Контурные линии, показывающие движение точек постоянной кривизны, движущиеся вдоль геодезических по направлению к базисной точке]] |
|||
Когда метрика на поверхности задана и базисная точка фиксирована, есть единственная геодезическая, соединяющая базисную точку с любой достаточно близкой точкой. Направление геодезической в базисной точке и расстояние единственным образом определяют другие точки. Эти две величины, направление и значение, тогда определяют касательный вектор в базисной точке. Отображение из касательных векторов к конечным точкам гладким образом заметают окрестность базисной точки и определяет так называемое «экспоненциальное отображение», которое определяет локальные координаты карты в базисной точке. Выметаемая окрестность имеет свойства, похожие на свойства шаров в евклидовом пространстве, а именно, любые две точки на ней связаны единственной геодезической. Такое свойство называется «геодезической кривизной», а координаты называются «нормальными координатами». Явное вычисление нормальных координат может быть выполнено путём рассмотрения дифференциального уравнения, соответствующего геодезическим. Свойства выпуклости являются следствием [[Лемма Гаусса о геодезических|леммы Гаусса]] и её обобщений. Грубо говоря, эта лемма утверждает, что геодезические, начинающиеся в базисной точке, должны пересекать сферы фиксированного радиуса с центром в базисной точке под прямыми углами. Геодезические полярные координаты получаются при комбинации экспоненциального отображения с полярными координатами на касательных векторах в базисной точке. Гауссова кривизна поверхности тогда задаётся отклонением второго порядка метрики от евклидовой метрики. В частности, Гауссова кривизна является инвариантом метрики, знаменитая теорема Гаусса ''[[Theorema Egregium]]''. Удобный способ понимания кривизны приходит из обыкновенных дифференциальных уравнений, которые первым рассматривал Гаусс, а затем обобщил Якоби. Эти уравнения возникают из изменения нормальных координат двух различных точек. Уравнение Гаусса — Якоби даёт другой способ вычисления гауссовой кривизны. Геометрически оно объясняет, что произойдёт с геодезическими из фиксированной базисной точки, когда конечная точка перемещается вдоль маленького сегмента кривой. Поведение геодезической показывается через данные, записанные в [[поле Якоби]], [[Векторное поле|векторном поле]] вдоль геодезической{{sfn|doCarmo|1976|с=357}}. После одного с четвертью столетий после Гаусса и Якоби [[Морс, Марстон|Марстон Морс]] дал более концептуальную интерпретацию поля Якоби в терминах второй производной функции энергии на бесконечномерном [[гильбертово многообразие|гильбертовом многообразии]] путей{{sfn|Milnor|1963}}. |
|||
=== Экспоненциальное отображение === |
|||
{{Подробная статья|Нормальные координаты }} |
|||
Теория [[Обыкновенное дифференциальное уравнение|обыкновенных дифференциальных уравнений]] показывает, что если <math>f(t, v)</math> гладкая, то дифференциальное уравнение <math>\tfrac{dv}{dt} = f(t,v)</math> с начальным условием <math>v(0) = v_0</math> имеет единственное решение для достаточно малых <math>|t|</math> и это решение зависит гладко от {{math|''t''}} и <math>v_0</math>. Из этого следует, что для достаточно малых [[Касательный вектор|касательных векторов]] {{math|''v''}} в заданной точке <math>p = (x_0,y_0)</math> существует геодезическая <math>c_v(t)</math>, определённая на (−2,2) с <math>c_v(0) = (x_0,y_0)</math> и <math>\dot c _v(0) = v</math>. Боле того, если <math>|s| \leqslant 1</math>, то <math>c_{sv} = c_v(st)</math>. '''[[Экспоненциальное отображение]]''' задаётся выражением |
|||
:<math>\exp_p(v) = c_v</math> (1) |
|||
и даёт диффеоморфизм между кругом <math>\|v\|< \delta</math> и окрестностью точки {{math|''p''}}. Более обще, отображение, переводящее {{math|(''p'',''v'')}} в <math>exp_p(v)</math>, даёт локальный диффеоморфизм в окрестности {{math|(''p'',''p'')}}. Экспоненциальное отображение даёт '''[[нормальные координаты]]''' вблизи {{math|''p''}}{{sfn|Wilson|2008}}. |
|||
=== Вычисление нормальных координат === |
|||
Существует стандартная техника (см, например, книгу Бергера{{sfn|Berger|2004}}) для вычисления изменений переменных от нормальных координат {{math|''u''}}, {{math|''v''}} в точке как разложение в формальный ряд Тейлора. Если координаты {{math|''x''}}, {{math|''y''}} в (0,0) локально ортогональны, запишем |
|||
:<math>x(u,v) = {\alpha}u + L(u,v) + \lambda(u,v) + \dots</math> |
|||
:<math>y(u,v) = {\beta}v + M(u,v) + \mu(u,v) + \dots</math> |
|||
где {{math|''L''}}, {{math|''M''}} квадратичные, а <math>\lambda</math>, <math>\mu</math> кубические однородные многочлены от {{math|''u''}} и {{math|''v''}}. Если {{math|''u''}} и {{math|''v''}} фиксированы, <math>x(t) = x(tu,tv)</math> и <math>y(t) = y(tu, tv)</math> могут рассматриваться как решения уравнений Эйлера в виде формальных степенных рядов — это единственным образом определяет <math>\alpha</math>, <math>\beta</math>, <math>L</math>, <math>M</math>, <math>\lambda</math> и <math>\mu</math>. |
|||
=== Лемма Гаусса === |
|||
{{Основная статья|Лемма Гаусса о геодезических}} |
|||
[[Файл:Polar coordinates grid.svg|thumb|right|В геодезических полярных координатах геодезические лучи из начала координат пересекают окружности постоянного радиуса ортогонально. Расстояния вдоль радиусов являются истинными расстояниями, но мадые дуги концентрических окружностей имеют длину <math>H(r,\theta) = G(r,\theta)^{\tfrac{1}{2}}</math> на угол, который они стягивают.]] |
|||
В этих координатах матрица {{math|''g''(''x'')}} удовлетворяет условию <math>g(0) = E</math> и прямые <math>t \mapsto tv</math> являются геодезическими через 0. Из равенства Эйлера вытекает матричное равенство |
|||
:<math>g(v)v = v</math>, |
|||
ключевой результат, обычно называемый [[Лемма Гаусса о геодезических|леммой Гаусса]]. Геометрически она утверждает, что |
|||
:{|border="1" cellspacing="0" cellpadding="5" |
|||
|'''''геодезические через 0 пересека.т окружности с центром в 0 [[Ортогональность|ортогонально]].''''' |
|||
|} |
|||
Если взять [[Полярная система координат|полярные координаты]] <math>(r,\theta)</math>, получаем, что метрика имеет вид |
|||
: <math>ds^2 = dr^2 + G(r,\theta) d\theta^2</math>. |
|||
В геодезических координатах легко проверить, что геодезические через нуль минимизируют длину. Топология на римановом многообразии задаётся [[Метрическое пространство|функцией расстояния]] <math>d(p,q)</math>, а именно, [[Точная верхняя и нижняя границы|нижней границей]] длин кусочногладких путей между {{math|''p''}} и {{math|''q''}}. Это расстояние реализуется геодезическими, так что в нормальных координатах <math>d(0,v) = \|v\|</math>. Если радиус <math>\delta</math> достаточно мал, слегка усиленная лемма Гаусса показывает, что образ {{math|''U''}} диска <math>\|v\|< \delta</math> при экспоненциальном отображении является [[Геодезическая кривизна|геодезической кривизной]], то есть любые две точки в {{math|''U''}} соединены единственной геодезической, лежащей полностью в {{math|''U''}}{{sfn|Berger|2004"}}{{sfn|do Carmo|1976|с=303–305}}. |
|||
=== Theorema Egregium === |
|||
{{Основная статья|Theorema Egregium}} |
|||
Если координаты {{math|''x''}} и {{math|''y''}} поверхности в <math>\mathbb{E}^3</math>, соответствующие <math>F(x,y) = k_1x^2 + k_2y^2 + \dots</math>, разложение в степенной ряд метрики задаётся в нормальных координатах {{math|(''u'', ''v'')}} как |
|||
:<math>ds^2 = du^2 + dv^2 + K(u dv - v du)^2 + \dots</math> |
|||
Этот экстраординарный результат — гауссова [[Theorema Egregium]] — показывает, что гауссова кривизна поверхности может быть вычислена исключительно в терминах метрики, а потому является внутренним инвариантом поверхности, не зависящим от любого вложения в <math>\mathbb{E}^3</math> и не меняющемся при преобразовании координат. В частности, изометрии поверхностей сохраняют Гауссову кривизну{{sfn|Berger|2004}}. |
|||
=== Уравнение Гаусса — Якоби === |
|||
{{Подробная статья|Поле Якоби}} |
|||
Если взять изменение нормальных координат в точке {{math|''p''}} к нормальным координатам в близкой точке {{math|''q''}}, получаем [[Задача Штурма — Лиувилля|уравнение Штурма — Лиувилля]] при <math>H(r,\theta) = G(r,\theta)^{\tfrac{1}{2}}</math>, открытое Гауссом и [[Поле Якоби|позднее обобщенное]] [[Якоби, Карл Густав Якоб|Густавом Якоби]], |
|||
:{|border="1" cellspacing="0" cellpadding="5" |
|||
|<math>H_{rr} = - KH</math> |
|||
|} |
|||
[[Матрица Якоби|Якобиан]] изменения этих координат в точке {{math|''q''}} равен <math>H_r</math>. Это даёт другой способ определения внутренней природы гауссовой кривизны. Поскольку <math>H(r, \theta)</math> можно интерпретировать как длину элемента линии в направлении <math>\theta</math>, уравнение Гаусса — Якоби показывает, что гауссова кривизна измеряет распространение геодезических на геометрической поверхности при удалении от точки{{sfn|O'Neill|1997|с=395}}. |
|||
=== Оператор Лапласа–Белтрами === |
|||
На поверхности с локальной метрикой |
|||
:<math> ds^2 = E \, dx^2 + 2F \, dx \, dy + G \, dy^2 </math> |
|||
и [[оператор Лапласа — Бельтрами|оператором Лапласа — Бельтрами|]] |
|||
:<math>\Delta f = {1\over H} \left(\partial_x {G\over H} \partial_x f - \partial_x {F\over H}\partial_y f -\partial_y {F\over H}\partial_x f + \partial_y {E\over H}\partial_yf\right),</math> |
|||
где <math>H^2 = EG - F^2</math>, гауссова кривизна в точке задаётся формулой{{sfn|Helgason|1978|с=92}} |
|||
:<math> K=- 3 \lim_{r\rightarrow 0} \Delta (\log r),</math> |
|||
где {{math|''r''}} обозначает геодезическое расстояние от точки. Поскольку <math>\Delta</math> является внутренним инвариантом, это даёт ещё одно доказательство, что гауссова кривизна является внутренним инвариантом. |
|||
В [[Изотермическая система координат|изотермической системе координат]], которую первым рассматривал Гаусс, требуется, чтобы метрика была специального вида |
|||
:<math>ds^2 = e^\varphi (dx^2+dy^2). \, </math> |
|||
В этом случае оператор Лапласа — Бельтрами задаётся выражением |
|||
:<math>\Delta = e^{-\varphi} \left(\frac{\partial^2 }{\partial x^2} + \frac{\partial^2 }{\partial y^2}\right)</math> |
|||
и <math>\varphi</math> удовлетворяет [[Теорема Лиувилля о сохранении фазового объёма|уравнению Лиувилля]]{{sfn|O'Niell|1997|с=286}} |
|||
:<math>\Delta \varphi=-2K. \, </math> |
|||
Известно, что изотермические системы координат существуют в окрестности любой точки поверхности, хотя все проверки на сегодняшний день опираются на нетривиальные результаты из области [[Дифференциальное уравнение в частных производных|дифференциальных уравнений в частных производных]]{{sfn|do Carmo|1976|с=227}}. Существует элементарное доказательство для минимальной поверхности{{sfn|Osserman|2002|с=31–32}}. |
|||
== Теорема Гаусса — Бонне == |
|||
[[Файл:Toroidal polyhedron.gif|thumb|right|Триангуляция [[Тор (поверхность)|тора]]]] |
|||
На [[Сфера|сфере]] или [[гиперболоид]]е площадь геодезического |
|||
треугольника, то есть треугольника, все стороны которого являются геодезическими, пропорциональна разнице сумм внутренних углов с <math>\pi</math>. Константа пропорциональности является просто гауссовой кривизной, постоянной для этих поверхностей. Для тора разность равна нулю, что отражает факт, что его гауссова кривизна равна нулю. Это стандартные результаты в сферической, гиперболической и высшей тригонометрии (см. ниже). Гаусс обобщил эти результаты на произвольные поверхности показав, что интеграл гауссовой кривизны по внутренности геодезического треугольника равен его угловой невязке (нехватке или избытке). Его формула показала, что гауссова кривизна может быть вычислена близ точки как предел площади по угловой невязке для геодезических треугольников, стягивающихся к точке. Поскольку любая замкнутая поверхность может быть разбита на геодезические треугольники, формула может быть использована для вычисления интеграла кривизны по всей поверхности. Как специальный случай того, что сейчас называется [[Формула Гаусса — Бонне|теоремой Гаусса — Бонне]], Гаусс доказал, что этот интеграл всегда равен <math>2\pi</math> на целое число, топологический инвариант поверхности, называемый [[Эйлерова характеристика|эйлеровой характеристикой]]. Этот инвариант легко вычисляется в терминах числа вершин, рёбер и граней треугольников в разбиении, которое называется [[Триангуляция (топология)|триангуляцией]]. Эта связь анализа и топологии была предвестником многих более поздних результатов в геометрии, достигших апогея в [[Теорема Атьи — Зингера об индексе|теореме Атьи — Зингера об индексе]]. В частности, свойства кривизны накладывают ограничения на топологию поверхности. |
|||
=== Геодезические треугольники === |
|||
Гаусс доказал, что кагда <math>\Delta</math> является геодезическим треугольником на поверхности с углами <math>\alpha</math>, <math>\beta</math> и <math>\gamma</math> в вершинах {{math|''A''}}, {{math|''B''}} и {{math|''C''}}, то |
|||
:<math>\int_\Delta K\,dA = \alpha + \beta + \gamma - \pi.</math> |
|||
Фактически, принимая геодезические полярные координаты в начале координат {{math|''A''}} и {{math|''AB''}}, {{math|''AC''}} радиусы с полярными углами 0 и <math>\alpha</math>: |
|||
:<math>\begin{align} |
|||
\int_\Delta K\,dA &= \int_\Delta KH\,dr\,d\theta = - \int_0^\alpha \int_0^{r_\theta} \! H_{rr}\,dr\,d\theta \\ |
|||
&= \int_0^\alpha 1 -H_r(r_\theta,\theta)\,d\theta = \int_0^\alpha d\theta + \int_{\pi-\beta}^\gamma \!\! d\varphi \\ |
|||
&= \alpha + \beta + \gamma - \pi, |
|||
\end{align}</math> |
|||
где второе равенство вытекает из равенства Гаусса — Якоби, а четвёртое из формулы производной Гаусса в ортогональной системе координат <math>(r, \theta)</math>. |
|||
Формула Гаусса показывает, что кривизна в точке может быть вычислена как предел ''угловой невязки'' <math>\alpha + \beta + \gamma - \pi</math> по ''площади'' для всё более маленьких геодезических треугольников рядом с точкой. Качественно поверхность положительно или отрицательно выгнута согласно знаку угловой невязки для произвольно маленьких геодезических треугольников{{sfn|Levi-Civita|1917}} |
|||
=== Теорема Гаусса — Бонне === |
|||
[[Файл:Icosahedron.svg|thumb|right|Эйлерова характеристика сферы, триангулированной как [[икосаэдр]], равна <math>V - E + F = 12 - 30 + 20 = 2</math>.]] |
|||
{{Основная статья|Формула Гаусса — Бонне}} |
|||
Поскольку любое компактное ориентированное 2-многообразие {{math|''M''}} может быть [[Триангуляция (топология)|триангулировано]] маленькими геодезическими треугольниками, отсюда следует, что |
|||
:<math> \int_M K dA = 2\pi\,\chi(M)</math> |
|||
где <math>\chi(M)</math> означает [[Эйлерова характеристика|эйлерову характеристику]] поверхности. |
|||
Фактически, если есть {{math|''F''}} граней, {{math|''E''}} рёбер и {{math|''V''}} вершин, то <math>3F = 2E</math> и левая часть равна <math>2{\pi}V - {\pi}F = 2\pi(V - E + F) = 2\pi\chi(M)</math>. |
|||
Это знаменитая '''[[Формула Гаусса — Бонне|теорема Гаусса — Бонне]]'''. Она показывает, что интеграл гауссовой кривизны равен топологическому инварианту многообразия, а именно, эйлеровой характеристике. Эту теорему можно интерпретировать многими способами. Возможно, одной из наиболее далеко идущих интерепретаций служит теорема для [[Эллиптический оператор|эллиптического дифференциального оператора]] на {{math|''M''}}, один из простейших случаев [[Теорема Атьи — Зингера об индексе|теоремы Атьи — Зингера об индексе]]. Другой связанный результат, который может быть доказан с помощью теоремы Гаусса — Бонне, это [[теорема Пуанкаре о векторном поле]] для векторных полей на многообразии {{math|''M''}}, которые принимают значение ноль лишь на конечном числе точек — сумма индексов в этих точках равна эйлеровой характеристике, где ''индекс'' точки определяется следующим образом: на малой окружности вокруг изолированного нуля векторное поле определяет отображение в единичную окружность, индекс равен просто [[Порядок точки относительно кривой|порядку точки]] этого отображения.) {{sfn|Levi-Civita|1917}} |
|||
=== Кривизна и вложения === |
|||
Если гауссова кривизна поверхности {{math|''M''}} везде положительна, то эйлерова характеристика положительна, так что {{math|''M''}} гомеоморфна (а потому и диффеоморфна) <math>\mathbf{S}^2</math>. Если вдобавок поверхность изометрично вложена в <math>\mathbf{E}^3</math>, отображение Гаусса обеспечивает явный диффеоморфизм. Как заметил [[Адамар, Жак|Адамар]], в этом случае поверхность [[Выпуклое множество|выпукла]]. Этот критерий выпуклости можно рассматривать как двумерное обобщение хорошо известного критерия выпуклости плоской кривой по второй производной. [[Гильберт, Давид|Гильберт]] доказал, что любая изометрично вложенная замкнутая поверхность должна иметь точку с положительной кривизной. Таким образом, замкнутое риманово 2-многообразие неположительной кривизны никогда не может быть вложено изометрично в <math>\mathbf{E}^3</math>. Однако, как показал Адриано Гарсиа с помощью [[Изотермическая система координат#Уравнение Бельтрами|уравнения Бельтрами]] для {{не переведено 5|Квазикомформное отображение|квазикомформных отображений||quasiconformal mapping}}, это всегда возможно для некоторой {{не переведено 5|Конформная геометрия|кофмормной эквивалентности||conformal equivalence}}{{sfn|Singer, Thorpe|1967}}{{sfn|Garsia|1961|с= 93–110}}. |
|||
== Поверхности постоянной кривизны == |
|||
[[Односвязное пространство|Односвязные]] поверхности постоянной кривизны 0, +1 и –1 это евклидова плоскость, единичная сфера в <math>\mathbf{E}^3</math> и [[Геометрия Лобачевского|гиперболическая плоскость]]. Каждая из них имеет транзитивную трёхмерную [[Группа Ли|группу Ли]] сохраняющих ориентацию [[Изометрия (математика)|изометрий]] {{math|''G''}}, которая может быть использована для изучения геометрии поверхности. Каждая из двух некомпактных поверхностей может быть идентифицирована фактор-группой {{math|''G'' / ''K''}}, где {{math|''K''}} является [[Максимальная компактная подгруппа|максимальной компактной подгруппой]] группы {{math|''G''}}. Здесь {{math|''K''}} изоморфна [[U1|{{math|SO(2)}}]]. Любое другое замкнутое риманово 2-многообразие {{math|''M''}} постоянной гауссовой кривизны после умножения метрики на постоянную будет обязательно иметь одну из этих трёх поверхностей в качестве своего [[Накрытие|универсальное накрывающего пространства]]. В ориентированном случае [[фундаментальная группа]] <math>\Gamma</math> многообразия {{math|''M''}} может быть отождествлена с [[Решётка в группе|однородной подгруппой]] [[Кручение (алгебра)|без кручения]] группы {{math|''G''}}, а {{math|''M''}} может быть отождествлена с {{не переведено 5|двойной смежный класс|двойным смежным классом||double coset}} <math>\Gamma \backslash G / K</math>. В случае сферы и евклидовой плоскости единственно возможными примерами являются сама сфера и тор, полученный как фактор-группа {{math|'''R'''<sup>2</sup>}} по дискретным подгруппам ранга 2. Для замкнутых поверхностей [[Род поверхности|рода]] <math>g \geqslant 2</math>, [[пространство модулей]] римановых поверхностей, полученных при пробегании <math>\Gamma</math> по всем таким подгруппам, имеет вещественную размерность {{math|6''g'' − 6}}{{sfn|Imayoshi, Taniguchi|1992|с=47–49}}. По {{не переведено 5|Теорема об униформации|теореме об униформации||uniformization theorem}} Пуанкаре, любое ориентированное замкнутое 2-многообразие {{не переведено 5|Конформная геометрия|комформно эквивалентно||conformal equivalence}} поверхности постоянной кривизны 0, +1 или –1. Другими словами, при умножении метрики на положительную величину гауссова кривизна может быть приведена в точности к одному из этих значений (знаку [[Эйлерова характеристика|эйлеровой характеристики]] многообразия {{math|''M''}}){{sfn|Berger|1977}}{{sfn|Taylor|1996}}. |
|||
=== Евклидова геометрия === |
|||
[[Файл:Triangle with notations 2.svg|thumb|right|Треугольник на плоскости]] |
|||
В случае евклидовой плоскости группой симметрии является {{не переведено 5| евклидова группа|евклидова группа движений||Euclidean group}}, [[полупрямое произведение]] двуменой группы параллельных переносов на группу вращений{{sfn|Wilson|2008|с=1–23, Chapter I, ''Euclidean geometry''}}. Геодезическими являются прямые и геометрия закодирована в элементарные формулы [[Тригонометрия|тригонометрии]], такие как [[теорема косинусов]] для треугольника со сторонами {{math|''a''}}, {{math|''b''}}, {{math|''c''}} и углами <math>\alpha</math>, <math>\beta</math>, <math>\gamma</math>: |
|||
:<math> c^2 = a^2 +b^2 -2ab \,\cos \gamma.</math> |
|||
Плоский тор может быть получен как фактор-группа <math>\mathbb{R}^2</math> на [[Решётка в группе|решётку]], то есть свободную абелеву подгруппу ранга 2. Эти замкнутые поверхности не имеют изометрических вложений в <math>\mathbb{E}^3</math>. Тем не менее, они позволяют изометричные вложения в <math>\mathbb{E}^4</math>. В простейшем случае это следует из факта, что тор является произведением двух окружностей и может быть изометрично вложен в <math>\mathbb{E}^2</math>{{sfn|do Carmo|1976}}. |
|||
=== Сферическая геометрия === |
|||
{{см. также|Сферическая тригонометрия|Сферический треугольник}} |
|||
[[Файл:RechtwKugeldreieck.svg|thumb|right|Сферический треугольник]] |
|||
[[Файл:Spherical triangle 3d.png|thumb|right|Площадь [[Сферический треугольник|сферического треугольника]] на единичной поверхности равна <math>\alpha + \beta + \gamma - \pi</math>.]] |
|||
Группа изометрий единичной сферы <math>S^2</math> в <math>\mathbb{E}^3</math> является ортогональной группой {{math|[[O(3)]]}} с [[Группа вращений|группой вращений {{math|SO(3)}}]] в качестве подгруппы изометрий, сохраняющих ориентацию. Она является прямым произведением {{math|SO(3)}} на {{не переведено 5|антиподальное отображение|||antipodal map}}, переводящее {{math|''x''}} в {{math|–''x''}}{{sfn|Wilson|2008|с=25–49, Chapter II, ''Spherical geometry''}}. Группа {{math|SO(3)}} действует транзитивно на <math>S^2</math>. [[Действие группы|Подгруппа стабилизаторов]] единичного вектора (0,0,1) может быть отождествлено с {{math|SO(2)}}, так что <math>S^2 = SO(3)/SO(2)</math>. |
|||
Геодезические между двумя точками на сфере являются дугами [[Большой круг|большого круга]] с этими заданными конечными точками. Если точки не антиподальны, существует единственная кратчайшая геодезическая между точками. Геодезические могут быть описаны также с помощью теории групп — каждая геодезическая через северный полюс (0,0,1) является орбитой подгруппы вращений вокруг оси, проходящей через две антиподальные точки экватора. |
|||
'''[[Сферический треугольник]]''' — это геодезический треугольник на сфере. Он определяется точками {{math|''A''}}, {{math|''B''}} и {{math|''C''}} на сфере со сторонами {{math|''BC''}}, {{math|''CA''}} и {{math|''AB''}}, образованными дугами больших окружностей с длиной, меньшей <math>\pi</math>. Если длины сторон равны {{math|''a''}}, {{math|''b''}} и {{math|''c''}}, а углы между сторонами равны <math>\alpha</math>, <math>\beta</math> и <math>\gamma</math>, то [[Сферическая тригонометрия#Теоремы для произвольного сферического треугольника|сферическая теорема косинусов]] утверждает, что |
|||
:<math>\cos c = \cos a \, \cos b + \sin a\, \sin b \,\cos \gamma.</math> |
|||
Площадь треугольника задаётся формулой |
|||
:<math>Area = \alpha + \beta + \gamma - \pi</math>. |
|||
Используя [[Стереографическая проекция|стереографическую проекцию]] из северного полюса сфера может быть отождествлена с [[Расширенная комплексная плоскость|расширенной комплексной плоскостью]] <math>\mathbb{C} \cup \{\infty\}</math>. Явное отображение задаётся выражением |
|||
:<math>\pi(x,y,z)={x+iy\over 1-z}\equiv u + iv.</math> |
|||
При таком отображении любое вращение {{math|''S''<sup>2</sup>}} соответствует [[Преобразование Мёбиуса|преобразованию Мёбиуса]] в {{math|[[SU(2)]]}}, единственному с точностью до знака{{sfn|Wilson|2008|с=Chapter 2}}. По отношению к координатам {{math|(''u'', ''v'')}} на комплексной плоскости сферическая метрика превращается в{{sfn|Eisenhart|2004|с=110}} |
|||
:<math> ds^2 = {4(du^2 + dv^2)\over (1+u^2+v^2)^2}.</math> |
|||
Единичная сфера является единственной замкнутой ориентированной поверхностью с постоянной кривизной +1. Фактор-группа {{math|SO(3)/O(2)}} может быть отождествлена с [[Вещественная проективная плоскость|вещественной проективной плоскостью]]. Она не ориентирована и может быть описана как фактор-группа {{math|''S''<sup>2</sup>}} на антподальное отображение (умножение на −1). Сфера односвязна, в то время как вещественная проективная плоскость имеет фундаментальную группу {{math|'''Z'''<sub>2</sub>}}. [[Точечная группа в трёхмерном пространстве|Конечные подгруппы {{math|SO(3)}}]], соответствующие конечным подгруппам {{math|O(2)}} и группам симметрии [[Правильный многогранник|правильных многогранников]], не действуют свободно на {{math|''S''<sup>2</sup>}}, так что соответствующие частные не являются 2-многообразиями, а лишь [[орбифолд]]ами. |
|||
=== Гиперболическая геометрия === |
|||
{{см. также|Гиперболический треугольник|Геометрия Лобачевского}} |
|||
[[Файл:Poincare.jpg|thumb|right|upright|[[Пуанкаре, Анри|Анри Пуанкаре]] (1854-1912)]] |
|||
[[Неевклидова геометрия]]{{sfn|Stillwell|1990}}{{sfn|Bonola, Carslaw, Enriques|1955}} впервые обсуждалась в письмах Гаусса, который выполнил большие вычисления на исходе девятнадцатого века и, хотя в частном порядке письма посылались, он решил их не публиковать. В 1830 году [[Лобачевский, Николай Иванович|Лобачевский]] и, независимо, в 1832 году [[Бойяи, Янош|Бойяи]], сын математика, переписывавшегося с Гауссом, опубликовали синтетические версии новой геометрии, за которые их сильно критиковали. Однако это продолжалось лишь до 1868 года, когда Белтрами, а вслед за ним [[Клейн, Феликс|Кляйн]] в 1871 и Пуанкаре в 1882, дали конкретные аналитические модели теории, которой Кляйн дал название '''[[Геометрия Лобачевского|гиперболическая геометрия]]'''. Было представлено четыре модели 2-мерной гиперболической геометрии |
|||
* [[Проективная модель|Модель Бельтрами — Кляйна]]; |
|||
* [[Конформно-евклидова модель|Диск Пуанкаре]]; |
|||
* [[Верхняя полуплоскость|Верхняя полуплоскость Пуанкаре]]; |
|||
* [[Гиперболоидная модель]] [[Киллинг, Вильгельм|Вильгельма Киллинга]] в трёхмерном [[Пространство Минковского|пространстве Минковского]]. |
|||
Первая модель на основе диска имеет преимущество в том, что геодезические являются отрезками прямой (то есть, пересечениями евклидовых прямых с открытым единичным диском). Вторая модель имеет преимущество в том, что она даёт полную параллель с единичной сферой в 3-мерном евклидовом пространстве. Ввиду приложений в комплексном анализе и геометрии, однако, модели Пуанкаре употребляются наиболее часто. Модели взаимозаменяемы благодаря преобразованиям Мёбиуса между диском и верхней полуплоскостью. |
|||
Пусть |
|||
:<math>D=\{z\,\colon|z|<1\}</math> |
|||
будет [[Конформно-евклидова модель|диском Пуанкаре]] на комплексной плоскости с [[Метрика Пуанкаре|метрикой Пуанкаре]] |
|||
:<math>ds^2= {4(dx^2 +dy^2)\over (1-x^2-y^2)^2}.</math> |
|||
В полярных координатах <math>(r, \theta)</math> метрика задаётся выражением |
|||
:<math> ds^2= {4(dr^2 + r^2\, d\theta^2)\over (1-r^2)^2}.</math> |
|||
Длина кривой <math>\gamma\colon[a,b] \to D</math> задаётся формулой |
|||
:<math>\ell(\gamma)=\int_a^b {2|\gamma^\prime(t)|\, dt\over 1 -|\gamma(t)|^2}.</math> |
|||
Группа <math>G = SU(1,1)</math>, заданная как |
|||
:<math>G=\left\{ \begin{pmatrix} |
|||
\alpha & \beta \\ |
|||
\overline{\beta} & \overline{\alpha} |
|||
\end{pmatrix} : \alpha,\beta\in\mathbf{C},\,|\alpha|^2 -|\beta|^2=1 \right\}</math> |
|||
действует транзитивно посредством [[Преобразование Мёбиуса|преобразований Мёбиуса]] на {{math|''D''}}, а [[Действие группы#стабилизаторы|стабилизатор подгруппы]] 0 является группой вращений |
|||
:<math> K=\left\{ \begin{pmatrix} |
|||
\zeta & 0 \\ |
|||
0 & \overline{\zeta} |
|||
\end{pmatrix} : \zeta\in\mathbf{C},\,|\zeta|=1 \right\}.</math> |
|||
Факторгруппа {{math|SU(1,1)/±''E''}} является группой сохраняющих ориентацию изометрий круга {{math|''D''}}. Любые две точки {{math|''z''}} и {{math|''w''}} в {{math|''D''}} соединены единственной геодезической, которая представлена куском окружности или прямой, проходящих через {{math|''z''}} и {{math|''w''}} и ортогональных границе круга. Расстояние между {{math|''z''}} и {{math|''w''}} задаётся формулой |
|||
:<math>d(z,w)=2 \mathrm{th}\, ^{-1} \frac{|z-w|}{|1-\overline{w}z|}.</math> |
|||
В частности <math>d(0,r) = 2 \mathrm{th}\, ^{-1}r</math> и <math>c(t) = \tfrac{1}{2} \mathrm{th}\, t</math> является геодезической через 0 вдоль вещественной оси, параметризованной длиной дуги. |
|||
Топология, определённая данной метрикой эквивлентна обычной евклидовой топологии, хотя как метрическое пространство {{math|(''D'',''d'')}} оно полно. |
|||
[[Файл:Triangolo iperbolico.svg|thumb|right|Гиперболический треугольник в модели Пуанкаре]] |
|||
[[Гиперболический треугольник]] является геодезическим треугольником для этой метрики — любые три точки в {{math|''D''}} являются вершинами гиперболического треугольника. Если стороны имеют длины {{math|''a''}}, {{math|''b''}} и {{math|''c''}} с соответствующими углами <math>\alpha</math>, <math>\beta</math> и <math>\gamma</math>, то гиперболическая теорема косинусов утверждает, что |
|||
:<math> \mathrm{ch}\,c = \mathrm{ch}\,a\, \mathrm{ch}\,b - \mathrm{sh}\,a \, \mathrm{sh}\,b \,\cos \gamma.</math> |
|||
Площадь гиперболического треугольника задаётся равенством{{sfn|Wilson|2008|с=Chapter 5}} |
|||
:<math>Area = \pi - \alpha - \beta - \gamma</math>. |
|||
Единичный диск и верхняя полуплоскость |
|||
:<math>H=\{w=x+iy \,\colon\, y >0\}</math> |
|||
конформно эквивалентны по преобразованиям Мёбиуса |
|||
:<math> w=i {1+z\over 1-z},\,\, z={w-i\over w+i}.</math> |
|||
При таком отображении действие {{math|SL(2,R)}} преобразований Мёбиуса на {{math|''H''}} соответствует действию {{math|SU(1,1)}} на {{math|''D''}}. Метрика на {{math|''H''}} становится |
|||
:<math> ds^2 = {dx^2 + dy^2\over y^2}.</math> |
|||
Поскольку прямые или окружности сохраняются при преобразованиях Мёбиуса, геодезические снова описываются прямыми или окружностями, ортогональными вещественной оси. |
|||
Единичный диск с метрикой Пуанкаре является единственным односвязным ориентированным 2-мерным римановым многообразием с постоянной кривизной −1. Любая ориентированная замкнутая поверхность {{math|''M''}} с таким свойством имеет {{math|''D''}} в качестве универсального накрывающего пространства. Его [[фундаментальная группа]] может быть отождествлена с кокомпактной подгруппой без кручений <math>\Gamma</math> группы {{math|SU(1,1)}} таким образом, что |
|||
:<math> M= \Gamma\backslash G /K.</math> |
|||
В этом случае <math>\Gamma</math> является [[Задание группы|конечно представимой группой]]. Образующие и отношения закодированы в геодезической кривизне {{не переведено 5|фундаментальный многоугольник|фундаментального геодезического многоугольника||fundamental polygon}} в {{math|''D''}} (или {{math|''H''}}), геометрически соответствующего замкнутой геодезической на {{math|''M''}}. |
|||
'''Примеры'''. |
|||
* [[Поверхность Больцы]] рода 2; |
|||
* {{не переведено 5|Квартика Кляйна|||Klein quartic}} рода 3; |
|||
* [[Поверхность Макбита]] рода 7; |
|||
* {{не переведено 5|Первая тройка Гурвица|||First Hurwitz triplet}} рода 14. |
|||
=== Теорема об униформации === |
|||
{{см. также|Теорема об униформации}} |
|||
Если дана ориентированная замкнутая поверхность {{math|''M''}} с гауссовой кривизной {{math|''K''}}, метрика на {{math|''M''}} может быть изменена конформно путём умножения её на множитель <math>e^{2u}</math>. Новая гауссова кривизна {{math|''K′''}} тогда задаётся формулой |
|||
:<math>K^\prime(x)= e^{-2u} (K(x) - \Delta u),</math> |
|||
где <math>\Delta</math> является лапласианом исходной метрики. Тогда для того, чтобы показать, что заданная поверхность конформно эквивалентна метрике с постоянной кривизной <math>K'</math>, достаточно решить следующий вариант [[Теорема Лиувилля о сохранении фазового объёма|уравнения Лиувилля]]: |
|||
:<math>\Delta u = K^\prime e^{2u} + K(x).</math> |
|||
Если {{math|''M''}} имеет эйлерову характеристику 0, то она диффеоморфна [[тор]]у, <math>K' = 0</math>, так что это сводится к решению |
|||
:<math> \Delta u = K(x).</math> |
|||
Согласно стандартной эллиптической теории это возможно, поскольку интеграл {{math|''K''}} над {{math|''M''}} равен нулю по теореме Формула Гаусса — Бонне{{sfn|Taylor|1996b|с=107}}{{sfn|Berger|1977|с=341–343}}. |
|||
Когда {{math|''M''}} имеет отрицательную эйлерову характеристику, <math>K' = -1</math>, так что уравнение принимает вид |
|||
:<math>\Delta u = -e^{2u} + K(x).</math> |
|||
Если использовать непрерывность экспоненциального отображения на [[Пространство Соболева|пространстве Соболева]], согласно Нейлу Трюдингеру это нелинейное уравнение может всегда быть решено{{sfn|Berger|1977|с=222–225}}{{sfn|Taylor|1996b|с=101–108}}. |
|||
Наконец, в случае 2-сферы, <math>K = 1</math> и уравнение превращается в |
|||
:<math>\Delta u = e^{2u} + K(x).</math> |
|||
Хотя это нелинейное уравнение не решено прямо, из классических результатов, таких как [[теорема Римана — Роха]], вытекает, что оно всегда имеет решение{{sfn|Taylor|1996b}}. Метод [[Поток Риччи|потоков Риччи]], разработанные [[Гамильтон, Ричард (математик)|Ричардом Гамильтоном]], даёт другое доказательство существования на основе нелинейных [[Дифференциальное уравнение в частных производных|дифференциальных уравнений в частных производных]]{{sfn|Chow|1991}}. Фактически, поток Риччи на конформных метриках на <math>S^2</math> определяется на функциях <math>u(x, t)</math> выражением |
|||
:<math> u_t = 4\pi - K'(x,t) = 4\pi -e^{-2u} (K(x) - \Delta u). </math> |
|||
Чоу показал, что за конечное время {{math|''K′''}} становится положительным. Отталкиваясь от предыдущих результатов, Гамильтона мог бы теперь показать, что {{math|''K′''}} сходится к +1<ref>Чен, Лу и Тянь {{harv|Chen, Lu, Tian|2006}} указали на отсутствующий шаг в подходе Гамильтона и Чоу и подправили их подход. См. статью Эндрюса и Брайана {{harv|Andrews|Bryan|2009}}.</ref>. Ещё до этих результатов по потокам Риччи Осгуд, Филлипс и Сарнак{{sfn|Osgood, Phillips, Sarnak|1988}} дали альтернативный и технически более простой подход к униформизации, основываясь на потоке на римановых метриках {{math|''g''}}, определённой выражением <math>\log \det \Delta_g</math>. |
|||
Простое доказательство, использующее только эллиптические операторы, открытое в 1988, можно найти в статье Динга{{sfn|Ding|2001}}. Пусть {{math|''G''}} будет [[Функция Грина|функцией Грина]] на <math>S^2</math>, удовлетворяющая <math>{\Delta}G = 1 + 4\pi\delta_P</math>, где <math>\delta_P</math> является точечной мерой в фиксированной точке {{math|''P''}} поверхности <math>S^2</math>. Уравнение <math>{\Delta}v = 2K - 2</math> имеет гладкое решение {{math|''v''}}, поскольку правая сторона имеет интеграл 0 по теореме Гаусса — Бонне. Тогда <math>\varphi = 2G + v</math> удовлетворяет <math>\Delta\varphi = 2K</math> всегда на {{math|''P''}}. Отсюда следует, что <math>g_1 = e^{\varphi}g</math> является полной метрикой постоянной кривизны 0 на дополнении {{math|''P''}}, которая поэтому изометрична плоскости. В сочетании с [[Стереографическая проекция|стереографической проекцией]] из этого следует, что имеется гладкая функция {{math|''u''}}, такая что <math>e^{2u}g</math> имеет гауссову кривизну +1 на компоненте {{math|''P''}}. Функция {{math|''u''}} автоматически расширяется до гладкой функции на всей <math>S^2</math>.{{efn|1=Это следует из аргументов, вовлекающих теорему Сакса и Уленбека{{sfn|Sacks, Uhlenbeck|1981}} об устранимых особенностях {{не переведено 5|Гармоничное отображение|гармоничных отображений||harmonic map}} конечной энергии.}} |
|||
== Поверхности неположительной кривизны == |
|||
В области, где кривизна удовлетворяет <math>K \leqslant 0</math>, геодезические треугольники удовлетворяют {{не переведено 5|Пространство CAT(k)|CAT(0)||CAT(k) space}} неравенству '''геометрии сравнения''', которую изучали [[Картан, Эли Жозеф|Картан]], [[Александров, Александр Данилович|Александров]] и [[Топоногов, Виктор Андреевич|Топоногов]], и рассматривали позже с {{не переведено 5|Ансамбль Брюа–Титса|другой точки зрения||Bruhat–Tits building}} {{не переведено 5|Брюа, Франсуа|Брюа||François Bruhat}} и [[Титс, Жак|Титс]]. Благодаря [[Громов, Михаил Леонидович|Громову]] это описание неположительной кривизны в терминах лежащего в основе метрического пространства имело глубокое влияние на современную геометрию и, в частности, на [[Геометрическая теория групп|геометрические теории групп]]. Много результатов, известных для гладких поверхностей и их геодезических, такие как метод Биркгофа построения геодезических путём применения его процесса укорочения кривой или теорема Мангольдта и Адамара, что [[Односвязное пространство|односвязная]] поверхность неположительной кривизны гомеоморфна плоскости, остаются верными для этих более общих условиях. |
|||
=== Неравенство сравнения Александрова === |
|||
[[Файл:Median diagram.svg|thumb|right|[[Медиана треугольника|Медиана]] в треугольнике сравнения всегда длиннее, чем действительная медиана.]] |
|||
Простейший вид неравенства сравнения, впервые доказанного для поверхностей Александровым около 1940, утверждает, что |
|||
{{quotation|Расстояние между вершиной геодезического треугольника и средней точкой противоположной стороны всегда меньше, чем соответствующее расстояние в треугольнике сравнения на плоскости с теми же длинами сторон.}} |
|||
Неравенство следует из факта, что если {{math|''c''(''t'')}} описывает геодезическую, параметризованную длиной дуги, а {{math|''a''}} является фиксированной точкой, то |
|||
:<math>f(t) = d(a,c(t))^2 - t^2</math> |
|||
является [[Выпуклая функция|выпуклой функцией]], то есть |
|||
:<math>\ddot{f}(t) \geqslant 0.</math> |
|||
Если взять геодезические полярные координаты с началом в {{math|''a''}} так, что <math>\|c(t)\|= r(t)</math>, выпуклость эквивалентна |
|||
:<math> r\ddot{r} + \dot{r}^2 \geqslant 1.</math> |
|||
При переходе к нормальным координатам {{math|''u''}}, {{math|''v''}} на {{math|''c''(''t'')}} это неравенство превращается в |
|||
:<math>u^2 + H^{-1}H_rv^2 \geqslant 1</math>, |
|||
где <math>(u,v)</math> соответствует единичному вектору <math>\dot c(t)</math>. Это следует из неравенства <math>H_r \geqslant H</math>, следствие неотрицательности производной от [[вронскиан]]а от {{math|''H''}} и {{math|''r''}} в [[Задача Штурма — Лиувилля|теории Штурма — Лиувилля]]{{sfn|Berger|2004}}{{sfn|Jost|1997}}. |
|||
[[Файл:George David Birkhoff 1.jpg|thumb|right|upright|[[Биркгоф, Джордж Дэвид|Джордж Дэвид Биркгоф]] (1884–1944)]] |
|||
=== Существование геодезических === |
|||
На полной кривой поверхности любые две точки могут быть соединены геодезической. Это частный случай [[Теорема Хопфа — Ринова|теоремы Хопфа — Ринова]], которая также применима в более высоких размерностях. Предположение полноты автоматически выполняется для поверхности, которая вложена как замкнутое подмножество евклидова пространства. Однако, это больше не выполняется, если, например, мы удаляем изолированную точку с поверхности. Например, дополнение начала координат из евклидовой плоскости является примером неполной поверхности. В этом примере две точки, диаметрально противоположные относительно начала координат не могут быть соединены геодезической без покидания плоскости без точки. |
|||
=== Теорема Мангольдта — Адамара === |
|||
Для замкнутых поверхностей неположительной кривизны [[Мангольдт, Ганс Карл Фридрих фон|фон Мангольдт]] (1881) и [[Адамар, Жак|Адамар]] (1898) доказали, что экспоненциальное отображение в точке является накрывающим, так что [[Накрытие|универсальным накрывающим пространством]] многообразия является <math>\mathbb{E}^2</math>. Этот результат обобщил на более высокие размерности [[Картан, Эли Жозеф|Картан]] и обычно упоминается этот результат как '''[[Теорема Адамара — Картана]]'''. Для поверхностей этот результат следует из трёх важных фактов{{sfn|do Carmo|1976}}{{sfn|Berger|2004}} |
|||
* Экспоненциальное отображение имеет ''ненулевой якобиан'' везде для поверхностей с отрицательной кривизной, следствие необращения в нуль <math>H_r</math>. |
|||
* Любая геодезическая является ''бесконечно продолжаемой'', результат, известный как [[Теорема Хопфа — Ринова]] для {{math|''n''}}-мерных многообразий. В двухмерном случае, если геодезическая стремится к бесконечности в направлении точки {{math|''x''}}, замкнутый диск {{math|''D''}} с центром в близкой точке {{math|''y''}} с удалённой {{math|''x''}} может быть стянут в {{math|''y''}} вдоль геодезической, что топологически невозможно. |
|||
* Любые две точки в классе гомотопии ''связаны единственной геодезической'' (см. выше). |
|||
== Риманова связность и параллельный перенос == |
|||
{{Основная статья|Риманова связность на поверхности}} |
|||
[[Файл:Levi-Civita 1930.jpeg|thumb|right|upright|[[Леви-Чивита, Туллио|Туллио Леви-Чивита]] (1873-1941)]] |
|||
Классический подход Гаусса к дифференциальной геометрии поверхностей был стандартным элементарным подходом{{sfn|Eisenhart|2004}}{{sfn|Kreyszig|1991}}{{sfn|Berger|2004}}{{sfn|Wilson|2008}}, который предшествовал появлению концепций [[Риманово многообразие|римановых многообразий]], предложенных [[Риман, Бернхард|Бернхардом Риманом]] в середине девятнадцатого века и [[Связность (дифференциальная геометрия)|связности]], разработанной [[Леви-Чивита, Туллио|Туллио Леви-Чивита]], [[Картан, Эли Жозеф|Эли Картаном]] и [[Вейль, Герман|Германом Вейлем]] в начале двадцатого века. Понятие связности, [[Ковариантная производная|ковариантной производной]] и [[Параллельное перенесение|параллельного переноса]] дали более концептуальный и единообразный путь понимания кривизны, который не только позволил обобщения на многообразия более высоких размерностей, но и дал важное средство для определения новых геометрических инвариантов, называемых [[Характеристический класс|характеристическимм классами]]{{sfn|Kobayashi, Nomizu|1969|с=Chapter XII}}. Подходы, использующие ковариантные производные и связность были использованы в более современных книгах{{sfn|do Carmo|1976}}{{sfn|O'Neill|1997}}{{sfn|Singer, Thorpe|1967}}. |
|||
=== Ковариантная производная === |
|||
Связность поверхности можно определить различными эквивалентными путями, но с одинаково важными точками зрения. '''Связность Римана''' или '''[[связность Леви-Чивиты]]'''{{sfn|Levi-Civita|1917}} проще всего понять в терминах поднятия [[Векторное поле|векторных полей]], рассматриваемых как [[Дифференциальный оператор|дифференциальные операторы]] первого порядка, действующих на функциях на многообразиях, к дифференциальным операторам на [[Касательное расслоение|касательном расслоении]] или {{не переведено 5|Расслоение реперов|расслоении реперов||frame bundle}}. В случае вложенной поверхности подъём до оператора на векторных полях, называемый '''ковариантной производной''', очень просто описывается в терминаз ортогональной проекции. Более того, векторное поле на поверхности, вложенной в <math>\mathbb{R}^3</math>, может пониматься как функция из поверхности в <math>\mathbb{R}^3</math>. Другое векторное поле действует как оператор дифференцирования покомпонентно. Получающееся векторное поле не будет касательным к поверхности, но это можно исправить, взяв ортогональную проекцию в касательное пространство в каждой точке поверхности. [[Риччи-Курбастро, Грегорио|Риччи]] и [[Леви-Чивита, Туллио|Леви-Чивита]] осознали на исходе двадцатого века, что этот процесс зависит только от метрики и может быть локально выражен в терминах символов Кристоффеля. |
|||
[[Файл:Parallel Transport.svg|thumb|right|Параллельный перенос вектора по геодезическому треугольнику на сфере. Длина переносимого вектора и его угол с каждой из сторон остаётся постоянным.]] |
|||
=== Параллельный перенос === |
|||
'''[[Параллельное перенесение|Параллельный перенос]]''' касательных векторов вдоль кривой на поверхности был следующим важным шагом вперёд благодаря [[Леви-Чивита, Туллио|Леви-Чивита]] {{sfn|Levi-Civita|1917}}. Он связан с более ранним понятием ковариантной производной, поскольку является [[Монодромия|монодромией]] [[Обыкновенное дифференциальное уравнение|обыкновенного дифференциального уравнения]] на кривой, определённой ковариантной производной с учётом скорости вектора кривой. Параллельный перенос вдоль геодезических, «прямых» на плоскости, может также просто описан прямо. Вектор в касательной плоскости переносится вдоль геодезической как единственное векторное поле с постоянной длиной и имеющих постоянный угол со скоростью вектора геодезической. Для кривой общего вида этот процесс следует модифицировать с помощью геодезической кривизны, которая измеряет как далеко кривая отходит от геодезической{{sfn|Berger|2004}} |
|||
Векторное поле <math>v(t)</math> вдоль кривой единичной скорости <math>c(t)</math>, с геодезической кривизной <math>k_g(t)</math>, говорят, что параллельно вдоль кривой, если |
|||
* оно имеет постоянную длину |
|||
* угол <math>\theta(t)</math>, которое оно имеет с вектором скорости <math>\dot c(t)</math>, удовлетворяет уравнению |
|||
:<math>\dot{\theta}(t) = - k_g(t)</math> |
|||
Это возвращает правило параллельного переноса вдоль геодезической или кусочно геодезической кривой, поскольку в этом случае <math>k_g = 0</math>, так что угол <math>\theta(t)</math> остаётся постоянной на любом отрезке геодезической. Существование параллельного переноса следует из того, что <math>\theta(t)</math> может быт вычислена как [[интеграл]] геодезической кривизны. Поскольку это зависит непрерывно от <math>L^2</math> нормы <math>k_g</math>, отсюда следует, что параллельный перенос для произвольной кривой может быть получен как предел параллельного переноса на приближении кусочно-геодезических кривых{{sfn|Arnold|1989|с=301–306, Appendix I.}}{{sfn|Berger|2004|с=263–264}}. |
|||
Связь может быть тогда описана в терминах поднятия путей в многообразии к путям в касательном или ортогональном расслоении реперов, что формализует классическую теорию "[[Репер (геометрия)|подвижного репера]]{{sfn|Darboux|1887-96}}. Подъём петель вокруг точки приводит к [[группа голономии|группе голономии]] в этой точке. Гауссова кривизна в точке может быть извлечена из параллельного переноса вокруг убывающих петель в точке. Эквивалентно кривизна может быть вычислена прямо на инфинитезимальном уровне в терминах {{не переведено 5|Скобка Ли векторных полей|скобок Ли||Lie bracket of vector fields}} поднятых векторных полей. |
|||
[[Файл:Elie-Cartan-1904.png|thumb|upright|[[Картан, Эли Жозеф|Эли Картан]] в 1904 году]] |
|||
=== 1-форма связности === |
|||
Подход Картана и Вейля, использующий 1-формы связности на {{не переведено 5|Расслоение реперов|расслоении реперов||frame bundle}} поверхнсти {{math|''M''}}, даёт третий путь для понимания римановой связности. Они заметили, что параллельный перенос требует, чтобы путь на поверхности был поднят до пути в расслоении реперов так, что его касательные вектора лежат в специальном подпространстве коразмерности единица в трёхмерном касательном пространстве расслоения реперов. Проекция в это подпространство определяется дифференциальной 1-формой на ортонормальном расслоении реперов, '''[[форма связности|формой связности]]'''. Это позволяет закодировать свойства кривизны в [[Дифференциальная форма|дифференциальных формах]] на расслоении реперов и формулы, вовлекающих их [[Дифференциальная форма|дифференциальные формы]]. |
|||
Этот подход особенно прост для вложенной поверхности. Согласно результату Кобаяши{{sfn|Kobayashi|1956}} 1-форма связности на поверхности, вложенной в евклидово пространство <math>\mathbb{E}^3</math> является просто обратным образом отображения Гаусса 1-формы связности на <math>S^2</math>{{sfn|Kobayashi, Nomizu|1969}}. Использование отождествление <math>S^2</math> с [[Однородное пространство|однородным пространством]] <math>\mathrm{SO}(3)/\mathrm{SO}(2)</math>, 1-форм связности является просто компонентой [[Форма Маурера-Картана|1-формы Маурера-Картана]] на {{math|SO(3)}}{{sfn|Ivey, Landsberg|2003}}. |
|||
== Глобальная дифференциальная геометрия поверхностей == |
|||
Хотя описание кривизны использует только локальную геометрию поверхности, имеются важные глобальные аспекты, такие как [[Формула Гаусса — Бонне|теорема Гаусса — Бонне]], {{не переведено 5|Теорема об униформации|теоремы об униформации||uniformization theorem}}, теорема Мангольдта — Адамара и теорема вложенности. Есть другие важные аспекты глобальной геометрии поверхностей{{sfn|Berger|2004|с=145–161}}{{sfn|do Carmo|1976}}{{sfn|Chern|1967}}{{sfn|Hopf|1989}}. Они включают: |
|||
*'''[[Радиус инъективности]]''', определённый как наибольший {{math|''r''}}, такой что две точки на расстоянии, меньшим {{math|''r''}}, соединены единственной геодезической. Вильгельм Клингенберг доказал в 1959 году, что радиус инъективности замкнутой поверхности ограничен снизу минимумом из <math>\delta = \tfrac{\pi}{\sqrt{sup K}}</math> и длины наименьшей замкнутой геодезической. Это уточнённая теорема Бонне, который показал в 1855 году, что диаметр замкнутой поверхности положительной гауссовой кривизны всегда ограничен сверху величиной <math>\delta</math>. Другими словами, геодезическая реализующая метрическое расстояние между двумя точками не может иметь длину больше, чем <math>\delta</math>. |
|||
*'''Жёсткость'''. В 1927 году [[Кон-Фоссен, Стефан Эммануилович|Кон-Фоссен]] доказал, что два изометричных [[овал]]оида – замкнутые поверхности с положительной гауссовой кривизной – обязательно конгруэнтны по изометрии <math>\mathbb{E}^3</math>. Однако, замкнутая вложенная поверхность с положительной гауссовой кривизной и постоянной средней кривизной обязательно является сферой. Аналогично, замкнутая вложенная поверхность постоянной гауссовой кривизны должна быть сферой (Либман, 1899). [[Хопф, Хайнц|Хайнц Хопф]] показал в 1950 году, что замкнутая вложенная поверхность с постоянной средней кривизной и родом 0, то есть гомеоморфная сфере, обязательно является сферой. Пятью годами позже Александров удалил топологическое предположение. В 1980-х годах Венте построил [[Погружение (топология)|погруженный]] тор постоянной средней кривизны в евклидово 3-пространство. |
|||
*'''[[Гипотеза Каратеодори]]''': Гипотеза утверждает, что замкнутая выпуклая три раза дифференцируемая поверхность допускает по меньшей мере две [[Точка округления|точки округления]]. Первой работой по этой гипотезе была работа Ганса Гамбургера в 1924, который заметил, что гипотеза следует из следующего более строгого утверждения: Полуцелый индекс расслоения главной кривизны изолированной [[Точка округления|омбилики]] не превосходит единицы. |
|||
*'''Нулевая гауссова кривизна''': полная поверхность в <math>\mathbb{E}^3</math> с нулевой гауссовой кривизной должна быть цилиндром или плоскостью. |
|||
*'''Теорема Гильберта''' (1901): никакая полная поверхность с постоянной отрицательной кривизной не может быть [[Погружение (топология)|погружена]] изометрично <math>\mathbb{E}^3</math>. |
|||
[[Файл:TorusSystoleLoop.png|right|thumb|Shortest loop on a torus]] |
|||
*'''{{не переведено 5|гипотеза Вилмора|||Willmore conjecture}}'''. Эта гипотеза утверждает, что интеграл от квадрата средней кривизны тора, вложенного в <math>\mathbb{E}^3</math>, должен быть ограничен снизу величиной <math>2\pi^2</math>. Известно, что интеграл является инвариантом Мёбиуса. Гипотезу решили в 2012 Фернандо Кода Маркес и Андрк Невес{{sfn|Codá Marques|2014|с=683–782}}. |
|||
*'''[[Изопериметрическая задача|Изопериметрическая неравенства]]'''. В 1939 Шмидт доказал, что классическое изопериметрическое неравенство для кривых на евклидовой плоскости также верно на сфере или на гиперболической плоскости. А именно, он доказал, что среди всех замкнутых кривых, ограничивающих область фиксированной площади, периметр минимален, если кривая является окружностью в этой метрике. В размерности на единицу больше, известно, что среди всех замкнутых поверхностей в <math>\mathbb{E}^3</math>, возникающих как граница ограниченной области единичного объёма, площадь поверхности минимально у евклидова шара. |
|||
*'''{{не переведено 5|Систолы поверхности|Систолические неравенства для кривых на поверхностях||Systoles of surfaces}}'''. Если дана замкнутая поверхность, её {{не переведено 5|систолическая геометрия|систола||systolic geometry}} определяется как наименьшая длина любой не стягиваемой в точку кривой на поверхности. В 1949 году Лёвнер доказал {{не переведено 5|Неравенство тора Лёвнера|неравенство тора||Loewner's torus inequality}} для метрик на торе, а именно, что площадь тора, делённая на квадрат его систолы, ограничена снизу величиной <math>\tfrac{\sqrt{3}}{2}</math> с равенством в случае постоянной кривизны. Аналогичный результат даётся [[Неравенство Пу|неравенством Пу для вещественной проективной плоскости]] 1952 года с нижней границей <math>\tfrac{2}{\pi}</math>, также достижимой в случае постоянной кривизны. Для [[Бутылка Клейна|бутылки Клейна]], Блаттер и Бавард позднее получили нижнюю границу <math>\tfrac{\sqrt{8}}{\pi}</math>. Для замкнутой поверхности рода {{math|''g''}}, Хебда и Бугаро показали, что отношение ограничено снизу величиной <math>\tfrac{1}{2}</math>. Тремя годами позднее [[Громов, Михаил Леонидович|Михаил Громов]] нашёл нижнюю границу, которая с точностью до постоянного множителя равна <math>g^{\tfrac{1}{2}}</math>, хотя она не оптимальна. Асимптотически строгие верхняя и нижняя границы равны с точностью до постоянного множителя <math>\tfrac{g}{(\log g)^2}</math>. Границы нашли Громов и Бузер-Сарнак, их можно найти в статье Катца{{sfn|Katz|2007}}. Имеется также версия для метрики на сфере, в которой для систолы берётся длина наименьшей по длине [[Замкнутая геодезическая|замкнутой геодезической]]. Громов высказал гипотезу о нижней границе <math>\tfrac{1}{2\sqrt{3}}</math> в 1980 году, лучшим результатом на настоящее время является нижняя граница <math>\tfrac{1}{8}</math>, полученная Региной Ротман в 2006 году{{sfn|Rotman|2006|с=3041-3047}}. |
|||
== Что читать далее == |
|||
Одним из наиболее обширных вводных обзоров по теме с описанием истории развития от догауссовского периода до современности принадлежит Бергеру{{sfn|Berger|2004}}. Рассмотрение классической теории дано в книгах Айзенхарта{{sfn|Eisenhart|2004}}, Крейзига{{sfn|Kreyszig|1991}} и Штрука{{sfn|Struik|1988}}. Более современные одинаково иллюстрированные книги для студентов Грея, Аббен м Саламона{{sfn|Gray, Abbena, Salamon|2006}}, Пресли{{sfn|Pressley|2001}} и Вильсона{{sfn|Wilson|2008}} могут быть более доступными. Достаточное количество классической теории можно найти в книге Гильберта и Кон-Воссена{{sfn|Hilbert, Cohn-Vossen|1952}}. Более сложные обсуждения студенческого уровня с использованием {{не переведено 5|Риманова связность на поверхности|римановой связности на поверхности||Riemannian connection on a surface}} можно найти в статьях Сингера и Торпа{{sfn|Singer, Thorpe|1967}}, до Кармо{{sfn|do Carmo|1976}} и О’Нила{{sfn|O'Neill|1997}}. |
|||
== См. также == |
|||
*[[Поверхность Цолля]] |
|||
==Примечания== |
|||
{{notelist}} |
|||
{{примечания|2}} |
|||
==Литература== |
==Литература== |
||
{{refbegin|colwidth=30em}} |
|||
*{{статья |
|||
|автор=Fernando Codá Marques, André Neves |
|||
|ref=Marques, Neves |
|||
|заглавие=Min-Max theory and the Willmore conjecture |
|||
|издание=Annals of Mathematics |
|||
|том=179 |
|||
|выпуск=2 |
|||
|год=2014 |
|||
|doi=10.4007/annals.2014.179.2.6 |
|||
|jstor=24522767 |
|||
|arxiv=1202.6036 |
|||
}} |
|||
*{{статья |
|||
|автор=Rotman R. |
|||
|ref=Rotman |
|||
|год=2006 |
|||
|заглавие=The length of a shortest closed геодезической and the area of a 2-dimensional sphere |
|||
|издание=Proc. Amer. Math. Soc. |
|||
|выпуск=134 |
|||
}} |
|||
*{{статья |
|||
|ref=Garsia |
|||
|автор=Adriano M. Garsia |
|||
|заглавие=An imbedding of closed Riemann surfaces in Euclidean space |
|||
|издание=Comment. Math. Helv. |
|||
|том= 35 |
|||
|год= 1961 |
|||
|страницы= 93–110 |
|||
|doi=10.1007/BF02567009 |
|||
}} |
|||
*{{книга |
*{{книга |
||
|ref= Jost |
|||
|автор=Топоногов В. А. |
|||
|автор=Jürgen Jost |
|||
|заглавие=Nonpositive curvature: geometric and analytic aspects |
|||
|издательство=Birkhäuser |
|||
|год=1997 |
|||
|isbn=978-0-8176-5736-9 |
|||
|серия=Lectures in Mathematics, ETH Zurich |
|||
}} |
|||
*{{книга |
|||
|автор=[[Александров, Александр Данилович|Aleksandrov A.D.]], [[Залгаллер, Виктор Абрамович|Zalgaller V.A.]] |
|||
|ref=Aleksandrov, Zalgaller |
|||
|заглавие=Instrinsic Geometry of Surfaces |
|||
|том=15 |
|||
|серия=Translations of Mathematical Monographs |
|||
|издательство= American Mathematical Society |
|||
|год=1967 |
|||
}} |
|||
** Оригинал {{книга |
|||
|автор=А. Д. Александров, В. А. Залгаллер |
|||
|заглавие=Двумерные многообразия ограниченной кривизны (Основы внутренней геометрии поверхностей) |
|||
|серия=Тр. МИАН СССР |
|||
|год=1962 |
|||
|том=63 |
|||
|страницы=3–262 |
|||
}} |
|||
*{{статья |
|||
|автор=Ben Andrews, Paul Bryan |
|||
|ref=Andrews, Bryan |
|||
|заглавие=Curvature bounds by isoperimetric comparison for normalized Ricci flow on the two-sphere |
|||
|издание=Calc. Var. Partial Differential Equations |
|||
|том= 39 |
|||
|выпуск=3–4 |
|||
|год=2010 |
|||
|страницы= 419–428 |
|||
|doi=10.1007/s00526-010-0315-5 |
|||
|arxiv=0908.3606 |
|||
}} |
|||
*{{книга |
|||
|автор=[[Арнольд, Владимир Игоревич|Arnold V.I.]] |
|||
|ref=Arnold |
|||
|заглавие=Mathematical methods of classical mechanics |
|||
|издание=2nd |
|||
|серия=Graduate Texts in Mathematics |
|||
|том=60 |
|||
|издательство=Springer-Verlag |
|||
|место=New York |
|||
|год=1989 |
|||
|isbn=978-0-387-90314-9 |
|||
}} |
|||
**оригинал {{книга |
|||
|автор=Арнольд В.И. |
|||
|заглавие=Математические методы классической механики |
|||
|год=1974 |
|||
|ISBN=5-354-00341-5 |
|||
}} |
|||
*{{книга |
|||
|ref=Berger |
|||
|автор=Marcel Berger |
|||
|заглавие=A Panoramic View of Riemannian Geometry |
|||
|издательство=Springer-Verlag |
|||
|год=2004 |
|||
|isbn=978-3-540-65317-2 |
|||
}} |
|||
*{{книга |
|||
|ref=Berger |
|||
|автор=Melvyn S. Berger |
|||
|заглавие=Nonlinearity and Functional Analysis |
|||
|год=1977 |
|||
|издательство=Academic Press |
|||
|isbn=978-0-12-090350-4 |
|||
}} |
|||
*{{книга |
|||
|заглавие=Non-Euclidean Geometry: A Critical and Historical Study of Its Development |
|||
|автор=Roberto Bonola, Carslaw H. S., Enriques F. |
|||
|ref=Bonola, Carslaw, Enriques |
|||
|издательство= Dover |
|||
|год= 1955 |
|||
|isbn=978-0-486-60027-7 |
|||
}} |
|||
** см. также {{книга |
|||
|автор=Роберто Бонола |
|||
|заглавие=Неевклидова геометрия (Критико-историческое изследованiе ея развитiя |
|||
|год=1910 |
|||
|место=С.-Петербургъ |
|||
}} |
|||
*{{книга |
|||
|ref=Brendle |
|||
|автор=Simon Brendle |
|||
|заглавие=Ricci flow and the sphere theorem |
|||
|серия=Graduate Studies in Mathematics |
|||
|том=111 |
|||
|издательство= American Mathematical Society |
|||
|год= 2010 |
|||
|isbn= 978-0-8218-4938-5 |
|||
}} |
|||
*{{книга |
|||
|автор=[[Картан, Эли Жозеф|Élie Cartan]] |
|||
|ref=Cartan |
|||
|заглавие=Geometry of Riemannian Spaces |
|||
|издательство= Math Sci Press |
|||
|год=1983 |
|||
|cссылка=https://books.google.com/?id=-YvvVfQ7xz4C&printsec=frontcover&dq=geometry+of+riemannian+spaces+cartan |
|||
|isbn =978-0-915692-34-7 |
|||
}}; Перевод второго издания книги ''Leçons sur la géométrie des espaces de Riemann'' (1951). |
|||
** перевод {{книга |
|||
|автор=Э. Катан |
|||
|заглавие=Геометрия римановых пространств |
|||
|год=1936 |
|||
|место=Ленинград |
|||
|издательство=ОНТИ НКТЦ СССР |
|||
}} |
|||
*{{книга |
|||
|автор =[[Картан, Эли Жозеф|Élie Cartan]] |
|||
|ref=Cartan |
|||
|ссылка=http://ebooks.worldscinet.com/mathematics/9789812799715/preserved-docs/9789812799715.pdf |
|||
|заглавие=Riemannian Geometry in an Orthogonal Frame (from lectures delivered by É Cartan at the Sorbonne in 1926-27) |
|||
|издательство=World Scientific |
|||
|год=2001 |
|||
|isbn =978-981-02-4746-1 |
|||
}}. |
|||
*{{статья |
|||
|автор=Xiuxiong Chen, Peng Lu, Gang Tian |
|||
|заглавие=A note on uniformization of Riemann surfaces by Ricci flow |
|||
|издание= Proc. AMS |
|||
|том=134 |
|||
|год=2006 |
|||
|страницы=3391–3393 |
|||
|doi=10.1090/S0002-9939-06-08360-2 |
|||
|выпуск=11 |
|||
}} |
|||
*{{книга |
|||
|автор=Chern S. S. |
|||
|ref=Chern |
|||
|заглавие=Curves and Surfaces in Euclidean Spaces |
|||
|серия=MAA Studies in Mathematics |
|||
|издательство=Mathematical Association of America |
|||
|год=1967 |
|||
}} |
|||
*{{статья |
|||
|автор=Chow B. |
|||
|ref=Chow |
|||
|заглавие=The Ricci flow on a 2-sphere |
|||
|издание=J. Diff. Geom. |
|||
|год=1991 |
|||
|том=33 |
|||
|выпуск=2 |
|||
|страницы=325–334 |
|||
|doi=10.4310/jdg/1214446319 |
|||
}} |
|||
*{{книга |
|||
|автор=Richard Courant |
|||
|ref=Courant |
|||
|год=1950 |
|||
|заглавие=Dirichlet's Principle, Conformal Mapping and Minimal Surfaces |
|||
|isbn=978-0-486-44552-6 |
|||
|издательство=John Wiley & Sons |
|||
}} |
|||
** перевод {{книга |
|||
|автор=Р. Курант |
|||
|заглавие=Принцип Дирихле, конформные отображения и минимальные поверхности |
|||
|издательство=издательство иностранной литературы |
|||
|место=Москва |
|||
|год=1953 |
|||
}} |
|||
*{{книга |
|||
|ref=Darboux |
|||
|автор=[[Дарбу, Жан Гастон|Gaston Darboux]] |
|||
|заглавие=Leçons sur la théorie générale des surfaces |
|||
|издательство=Gauthier-Villars |
|||
|год=1887-96 |
|||
}} [http://www.hti.umich.edu/cgi/t/text/text-idx?c=umhistmath;idno=ABV4153.0001.001 Том I (1887)], [http://www.hti.umich.edu/cgi/t/text/text-idx?c=umhistmath;idno=ABV4153.0002.001 Том II (1915) <nowiki>[1889]</nowiki>], [http://www.hti.umich.edu/cgi/t/text/text-idx?c=umhistmath;idno=ABV4153.0003.001 Том III (1894)], [http://www.hti.umich.edu/cgi/t/text/text-idx?c=umhistmath;idno=ABV4153.0004.001 Volume IV (1896)]. |
|||
** перевод {{книга |
|||
|автор=Жан Гастон Дарбу |
|||
|заглавие=Лекции по общей теории поверхностей и геометрические приложения анализа бесконечно малых |
|||
|год=2013 |
|||
|место=Москва, Ижевск |
|||
}} т1: isbn=978-5-4344-0118-0 т2: isbn=978-5-4344-0119-7 т3: isbn=978-5-4344-0120-3, т4 isbn=978-5-4344-0121-0 |
|||
*{{статья |
|||
|автор =Ding W. |
|||
|ref=Ding |
|||
|заглавие=A proof of the uniformization theorem on S<sup>2</sup> |
|||
|издание=J. Partial Differential Equations |
|||
|том= 14 |
|||
|год=2001 |
|||
|страницы= 247–250 |
|||
}} |
|||
*{{книга |
|||
|ref=do Carmo |
|||
|автор =Manfredo P. do Carmo |
|||
|заглавие=Differential Geometry of Curves and Surfaces |
|||
|издательство=Prentice-Hall |
|||
|год=1976 |
|||
|isbn = 978-0-13-212589-5 |
|||
}} |
|||
** перевод {{книга |
|||
|автор=Манфредо до Кармо |
|||
|заглавие=Дифференциальная геометрия кривых и поверхностей |
|||
|место=Москва, Ижевск |
|||
|год=2013 |
|||
|isbn=978-5-4344-0150-0 |
|||
}} |
|||
*{{книга |
|||
|автор = Luther P. Eisenhart |
|||
|ref=Eisenhart |
|||
|заглавие=A Treatise on the Differential Geometry of Curves and Surfaces |
|||
|издательство=Dover |
|||
|год =2004 |
|||
|isbn = 978-0-486-43820-7 |
|||
}} [https://archive.org/details/treatonthediffer00eiserich Full 1909 text] |
|||
*{{книга |
|||
|автор = Luther P. Eisenhart |
|||
|ref=Eisenhart |
|||
|заглавие=An Introduction to Differential Geometry with Use of the Tensor Calculus |
|||
|издательство=Princeton University Press |
|||
|год=1947 |
|||
|серия=Princeton Mathematical Series |
|||
|том=3 |
|||
|isbn = 978-1-4437-2293-3 |
|||
}} |
|||
*{{статья |
|||
|заглавие=Recherches sur la courbure des surfaces |
|||
|first=[[Эйлер, Леонард|Leonhard Euler]] |
|||
|ref=Euler |
|||
|год=1760 |
|||
|издание=Mémoires de l'Académie des Sciences de Berlin |
|||
|том=16 |
|||
|страницы=119–143 |
|||
|ссылка=http://math.dartmouth.edu/~euler/pages/E333.html |
|||
}}. Дата публикации - 1767 |
|||
*{{статья |
|||
|автор=[[Эйлер, Леонард|Leonhard Euler]] |
|||
|ref=Leonhard Euler |
|||
|год=1771 |
|||
|заглавие=De solidis quorum superficiem in planum explicare licet |
|||
|издание=Novi Commentarii Academiae Scientiarum Petropolitanae |
|||
|том=16 |
|||
|ссылка=http://math.dartmouth.edu/~euler/pages/E419.html |
|||
|страницы=3–34 |
|||
}}. Дата публикации - 1772 |
|||
*{{книга |
|||
|автор=[[Гаусс, Карл Фридрих|Carl Friedrich Gauss]] |
|||
|ref=Gauss |
|||
|заглавие=General Investigations of Curved Surfaces of 1825 and 1827 |
|||
|ссылка= http://quod.lib.umich.edu/cgi/t/text/text-idx?c=umhistmath;idno=ABR1255 |
|||
|год=1902 |
|||
|издательство=Princeton University Library |
|||
}} |
|||
**{{книга |
|||
|ref=Gauss |
|||
|автор=Carl Friedrich Gauss |
|||
|заглавие=General Investigations of Curved Surfaces |
|||
|год=1965 |
|||
|издательство=Raven Press |
|||
|место=Hewlett, NY |
|||
|oclc=228665499 |
|||
}} |
|||
**{{книга |
|||
|ref=Gauss |
|||
|автор=Carl Friedrich Gauss |
|||
|заглавие=General Investigations of Curved Surfaces |
|||
|год=2005 |
|||
|издательство=Dover Publications |
|||
|место=Mineola, NY |
|||
|isbn=978-0-486-44645-5 |
|||
}} |
|||
*{{книга |
|||
|автор=Alfred Gray, Elsa Abbena, Simon Salamon |
|||
|ref=Gray, Abbena, Salamon |
|||
|заглавие=Modern Differential Geometry of Curves And Surfaces With Mathematica |
|||
|год=2006 |
|||
|isbn=978-1-58488-448-4 |
|||
|издательство=CRC Press |
|||
}} |
|||
*{{книга |
|||
|автор=Qing Han, Jia-Xing Hong |
|||
|ref=Han, Hong |
|||
|заглавие= Isometric Embedding of Riemannian Manifolds in Euclidean Spaces |
|||
|издатедьство= American Mathematical Society |
|||
|год= 2006 |
|||
|isbn= 978-0-8218-4071-9 |
|||
}} |
|||
*{{книга |
|||
|автор=Sigurdur Helgason |
|||
|ref=Helgason |
|||
|заглавие=Differential Geometry,Lie Groups, and Symmetric Spaces |
|||
|издательство= Academic Press, New York |
|||
|год=1978 |
|||
|isbn = 978-0-12-338460-7 |
|||
}} |
|||
** перевод {{книга |
|||
|серия=XX век. Математика и механика |
|||
|выпуск=11 |
|||
|автор=С. Хелгасон |
|||
|заглавие=Дифференциальная геометрия, группы Ли и симметрические пространства |
|||
|место=Москва |
|||
|издательство=Факториал Пресс |
|||
|год=2005 |
|||
|isbn=5-88688-076-3 |
|||
}} |
|||
* {{книга |
|||
|ref=Hilbert, Cohn-Vossen |
|||
|автор=[[Гильберт, Давид|David Hilbert]], [[Кон-Фоссен, Стефан Эммануилович|Stephan Cohn-Vossen]] |
|||
|заглавие=Geometry and the Imagination |
|||
|издательство=Chelsea |
|||
|место=New York |
|||
|издание=2nd |
|||
|isbn=978-0-8284-1087-8 |
|||
|год=1952 |
|||
}} |
|||
*{{книга |
|||
|автор=Heinz Hopf |
|||
|ref=Hopf |
|||
|заглавие=Lectures on Differential Geometry in the Large |
|||
|серия=Lecture Notes in Mathematics |
|||
|издательство=Springer-Verlag |
|||
|том=1000 |
|||
|год=1989 |
|||
|isbn=978-3-540-51497-8 |
|||
}} |
|||
*{{книга |
|||
|first=Y.|last=Imayoshi|first2=M.|last2=Taniguchi |
|||
|заглавие=An Introduction to Techmüller spaces |
|||
|издательство=Springer-Verlag |
|||
|год=1992 |
|||
|isbn=978-0-387-70088-5 |
|||
}} |
|||
*{{книга |
|||
|автор=Thomas A. Ivey, J.M. Landsberg |
|||
|ref=Ivey, Landsberg |
|||
|заглавие=Cartan for Beginners: Differential Geometry via Moving Frames and Exterior Systems |
|||
|серия=Graduate Studies in Mathematics |
|||
|том=61 |
|||
|год=2003 |
|||
|isbn=978-0-8218-3375-9 |
|||
|издательство=American Mathematical Society |
|||
}} |
|||
*{{статья |
|||
|автор=Howard Jacobowitz |
|||
|ref=Jacobowitz |
|||
|заглавие=Local Isometric Embeddings of Surfaces into Euclidean Four Space |
|||
|издание= Indiana Univ. Math. J. |
|||
|том=21 |
|||
|год=1972 |
|||
|страницы= 249–254 |
|||
|ссылка=http://www.iumj.indiana.edu/IUMJ/FULLTEXT/1972/21/21019 |
|||
|doi=10.1512/iumj.1971.21.21019 |
|||
|выпуск=3 |
|||
}} |
|||
*{{книга |
|||
|ref=Katz |
|||
|автор=Mikhail G. Katz |
|||
|заглавие=Systolic geometry and topology |
|||
|издательство=American Mathematical Society |
|||
|серия=Mathematical Surveys and Monographs |
|||
|isbn=978-0-8218-4177-8 |
|||
|год=2007 |
|||
|том=137 |
|||
}} |
|||
*{{статья |
|||
|автор==Shoshichi Kobayashi |
|||
|ref=Kobayashi |
|||
|заглавие=Induced connections and imbedded Riemannian space |
|||
|издание=Nagoya Math. J. |
|||
|год=1956 |
|||
|том=10 |
|||
|страницы= 15–25 |
|||
|doi=10.1017/S0027763000000052 |
|||
|doi-access=free |
|||
}} |
|||
*{{статья |
|||
|ref=Kobayashi |
|||
|автор=Shoshichi Kobayashi |
|||
|заглавие=Theory of connections |
|||
|издание=Annali di Matematica Pura ed Applicata |
|||
|серия=Series 4 |
|||
|том=43 |
|||
|страницы= 119–194 |
|||
|год=1957 |
|||
|doi=10.1007/BF02411907 |
|||
}} |
|||
*{{книга |
|||
|автор=Shoshichi Kobayashi, Katsumi Nomizu |
|||
|ref=Kobayashi, Nomizu |
|||
|заглавие=Foundations of Differential Geometry |
|||
|том=I |
|||
|издательство=Wiley Interscience |
|||
|год=1963 |
|||
|isbn=978-0-470-49648-0 |
|||
}} |
|||
*{{книга |
|||
|автор=Shoshichi Kobayashi, Katsumi Nomizu |
|||
|ref=Kobayashi, Nomizu |
|||
|заглавие=Foundations of Differential Geometry |
|||
|том=II |
|||
|издательство=Wiley Interscience |
|||
|год=1969 |
|||
|isbn=978-0-470-49648-0 |
|||
}} |
|||
*{{книга |
|||
|ref=Kreyszig |
|||
|автор=Erwin Kreyszig |
|||
|год=1991 |
|||
|заглавие=Differential Geometry |
|||
|isbn=978-0-486-66721-8 |
|||
|издательство=Dover |
|||
}} |
|||
*{{книга |
|||
|заглавие=Differential Geometry: Curves - Surfaces – Manifolds |
|||
|автор Wolfgang Kühnel |
|||
|ref=Kühnel |
|||
|издательство= American Mathematical Society |
|||
|год=2006 |
|||
|isbn=978-0-8218-3988-1 |
|||
}} |
|||
*{{статья |
|||
|ref=Levi-Civita |
|||
|автор=[[Леви-Чивита, Туллио|Tullio Levi-Civita]] |
|||
|заглавие=Nozione di parallelismo in una varietà qualunque |
|||
|издание= Rend. Circ. Mat. Palermo |
|||
|том= 42 |
|||
|год=1917 |
|||
|страницы= 173–205 |
|||
|doi=10.1007/BF03014898 |
|||
|ссылка=https://zenodo.org/record/1428456/files/article.pdf |
|||
}} |
|||
*{{книга |
|||
|ref= O'Neill |
|||
|автор=Barrett O'Neill |
|||
|заглавие = Elementary Differential Geometry |
|||
|издательство=Academic Press |
|||
|год=1997 |
|||
|isbn= 978-0-12-526750-2 |
|||
}} |
|||
*{{статья |
|||
|автор=Osgood B., Phillips R., Sarnak P. |
|||
|ref=Osgood, Phillips, Sarnak |
|||
|заглавие=Extremals of determinants of Laplacians |
|||
|издание=J. Funct. Anal. |
|||
|том= 80 |
|||
|год=1988 |
|||
|станицы= 148–211 |
|||
|doi= 10.1016/0022-1236(88)90070-5 |
|||
}} |
|||
*{{книга |
|||
|заглавие=A Survey of Minimal Surfaces |
|||
|автор=Robert Osserman |
|||
|ref= Osserman |
|||
|издательство= Dover |
|||
|год= 2002 |
|||
|isbn=978-0-486-49514-9 |
|||
}} |
|||
** см. также {{книга |
|||
|автор=Р. Оссерман |
|||
|заглавие=Минимальные поверхности |
|||
|издание=УМН |
|||
|том=22 |
|||
|выпуск=4(136) |
|||
|год=1967 |
|||
|страницы=55–136 |
|||
}} |
|||
* {{книга |
|||
|автор=[[Ian R. Porteous]] |
|||
|ref= Porteous |
|||
|год=2001 |
|||
|заглавие=Geometric Differentiation: for the intelligence of curves and surfaces |
|||
|издательство=[[Cambridge University Press]] |
|||
|isbn=0-521-00264-8 |
|||
}} |
|||
*{{статья |
|||
|автор=Позняк Э. Г. |
|||
|ref=Poznjak |
|||
|заглавие=Изометрические погружения двумерных римановых метрик в евклидовы пространства |
|||
|Издание=УМН |
|||
|том= 28 |
|||
|год=1973 |
|||
|страницы= 47–77 |
|||
|doi=10.1070/RM1973v028n04ABEH001591 |
|||
|выпуск=4 |
|||
}} |
|||
*{{книга |
|||
|автор=Andrew Pressley |
|||
|ref=Pressley |
|||
|заглавие=Elementary Differential Geometry |
|||
|серия=Springer Undergraduate Mathematics Series |
|||
|год=2001 |
|||
|isbn=978-1-85233-152-8 |
|||
|издательство=Springer-Verlag |
|||
}} |
|||
*{{статья |
|||
|автор=Sacks J., Karen Uhlenbeck |
|||
|ref=Sacks, Uhlenbeck |
|||
|заглавие=The existence of minimal immersions of 2-spheres |
|||
|издание=Ann. of Math. |
|||
|год=1981 |
|||
|том= 112 |
|||
|стрницы=1–24 |
|||
|doi=10.2307/1971131 |
|||
|выпуск=1 |
|||
|jstor=1971131 |
|||
}} |
|||
*{{книга |
|||
|автор=Isadore Singer, John A. Thorpe |
|||
|ref=Singer, Thorpe |
|||
|заглавие=Lecture Notes on Elementary Topology and Geometry |
|||
|издательство=Springer-Verlag |
|||
|год=1967 |
|||
|isbn=978-0-387-90202-9 |
|||
}} |
|||
*{{книга |
|||
|заглавие=Sources of Hyperbolic Geometry |
|||
|автор=John Stillwell |
|||
|ref=Stillwell |
|||
|издательство=American Mathematical Society |
|||
|год= 1996 |
|||
|isbn=978-0-8218-0558-9 |
|||
}} |
|||
*{{книга |
|||
|заглавие=Lectures on classical differential geometry: Second Edition |
|||
|автор=Dirk Jan Struik |
|||
|ref=Struik |
|||
|год= 1988 |
|||
|издательство= Dover |
|||
|isbn=978-0-486-65609-0 |
|||
}} |
|||
*{{книга |
|||
|автор=Michael E. Taylor |
|||
|ref=Taylor |
|||
|заглавие=Partial Differential Equations II: Qualitative Studies of Linear Equations |
|||
|издательство=Springer-Verlag |
|||
|год=1996a |
|||
|isbn=978-1-4419-7051-0 |
|||
}} |
|||
*{{книга |
|||
|автор=Michael E. Taylor |
|||
|ref=Taylor |
|||
|заглавие=Partial Differential Equations III: Nonlinear equations |
|||
|издательство=Springer-Verlag |
|||
|год=1996b |
|||
|isbn=978-1-4419-7048-0}} |
|||
*{{книга |
|||
|заглавие=Differential Geometry of Curves and Surfaces: A Concise Guide |
|||
|автор= [[Топоногов, Виктор Андреевич|Victor A. Toponogov]] |
|||
|ref=Toponogov |
|||
|год=2005 |
|||
|isbn=978-0-8176-4384-3 |
|||
|издательство=Springer-Verlag |
|||
}} |
|||
**{{книга |
|||
|автор=[[Топоногов, Виктор Андреевич|Топоногов, В. А.]] |
|||
|заглавие=Дифференциальная геометрия кривых и поверхностей |
|заглавие=Дифференциальная геометрия кривых и поверхностей |
||
|издательство=Физматкнига |
|||
|год=2012 |
|год=2012 |
||
|ссылка=http://www.fizmatkniga.ru/catalog/st-f2eeefeeedeee3eee2/product-5438/ |
|||
|ISBN=9785891552135}} |
|||
|издательство=Физматкнига |
|||
|isbn=978-5-89155-213-5 |
|||
}} |
|||
*{{книга |
|||
|ref=Valiron |
|||
|автор=Georges Valiron |
|||
|заглавие=The Classical Differential Geometry of Curves and Surfaces |
|||
|год=1986 |
|||
|издательство= Math Sci Press |
|||
|isbn=978-0-915692-39-2 |
|||
}} [https://books.google.com/books?id=IQXstKvWsHMC&printsec=frontcover&dq=valiron+surfaces&source=gbs_summary_r&cad=0 Full text of book] |
|||
*{{книга |
|||
|ref=Wilson |
|||
|автор=Pelham Wilson |
|||
|заглавие=Curved Space: From Classical Geometries to Elementary Differential Geometry |
|||
|издательство=Cambridge University Press |
|||
|год=2008 |
|||
|isbn=978-0-521-71390-0 |
|||
}} |
|||
{{refend}} |
|||
{{кривизна}} |
|||
{{rq|empty|sources}} |
|||
{{тензоры}} |
|||
{{Доперевести}} |
|||
[[Категория:Дифференциальная геометрия поверхностей]] |
[[Категория:Дифференциальная геометрия поверхностей]] |
||
{{rq|checktranslate|style|grammar}} |
|||
Версия от 20:16, 3 июля 2020

Дифференциальная геометрия поверхностей имеет дело с дифференциальной геометрией гладких поверхностей с различными дополнительными структурами, наиболее часто, с римановой метрикой. Поверхности всесторонне изучались с различных точек зрения — внешней, связанной с их вложением в евклидово пространство, и внутренней, отражающей свойства, определённые исключительно расстояниями внутри поверхности, полученными вдоль кривых на поверхности. Одной из исследованных фундаментальных концепций является кривизна Гаусса, впервые глубоко изучавшейся Карлом Фридрихом Гауссом[1], который показал, что кривизна является внутренним свойством поверхности, независящим от его изометричного вложения в евклидово пространство.
Поверхности естественным образом возникают как графики функций от пары переменных и иногда возникают в параметрической форме или как геометрические места точек, ассоциированные с пространственными кривыми. Важную роль в их изучении играют группы Ли (в духе эрлангенской программы), а именно группы симметрии евклидовой плоскости, сферы и гиперболической поверхности. Эти группы Ли могут быть использованы для описания поверхностей постоянной гауссовой кривизны. Они дают также существенный вклад в современные подходы к внутренней дифференциальной геометрии через связность. С другой стороны, внешние свойства, опирающиеся на вложение поверхности в евклидовом пространстве, также интенсивно изучались. Это хорошо иллюстрирует нелинейные уравнения Эйлера — Лагранжа в вариационном исчислении — хотя Эйлер рассматривал уравнения от одной переменной для понимания геодезических, определённых независимо от вложения, главные приложения уравнений от двух переменных были для минимальных поверхностей, концепции, которую можно определить только в терминах вложения.
Обзор
Многогранники в евклидовом пространстве, такие как граница куба, были среди первых поверхностей, с которыми встретилась геометрия. Можно также определить гладкие поверхности, в которых каждая точка имеет окрестность, диффеоморфную некоторой открытой поверхности в евклидовой плоскости. Это позволяет применять математический анализ к поверхностям для доказательства многих результатов.
Две гладкие поверхности диффеоморфны тогда и только тогда, когда они гомеоморфны. (Аналогичный результат не имеет место для многообразий размерности четыре и выше.) Отсюда следует, что замкнутые поверхности классифицируются с точностью до диффеоморфизма их эйлеровой характеристикой и ориентируемостью.
Гладкие поверхности, снабжённые римановыми метриками, имеют фундаментальную важность в дифференциальной геометрии. Риманова метрика снабжает поверхность понятиями геодезической, расстояния, угла и площади. Важным классом таких поверхностей является развёртывающиеся поверхности — поверхности, которые могут быть расправлены в плоскость без растяжений. Примеры включают цилиндр и конус.
Кроме того, есть свойства поверхностей, зависящие от вложения поверхности в евклидово пространство. Такие поверхности являются объектами рассмотрения внешней геометрии. К ним относятся
- Минимальные поверхности, это поверхности, которые минимизируют площадь поверхности для заданных краевых условий. Примеры включают мыльные плёнки, натянутые на проволочную рамку, катеноиды и геликоиды.
- Линейчатые поверхности, это поверхности, которые имеют для каждой точки лежащую на поверхности по меньшей мере одну прямую, проходящую через эту точку. Примеры включают цилиндры и однолистные гиперболоиды.
Любое n-мерное комплексное многообразие является, в то же время, 2n-мерным вещественным многообразием. Тогда любой комплексный одно-многообразие (называемое также римановой поверхностью) является гладкой ориентированной поверхностью с ассоциированной комплексной структурой[англ.]. Любая замкнутая поверхность допускает комплексные структуры. Любая комплексная алгебраическая кривая или вещественная алгебраическая поверхность является также гладкой поверхностью, возможно, с сингулярностями.
Комплексные структуры на замкнутой ориентированной поверхности соответствуют классам комформной эквивалентности[англ.] римановых метрик на поверхности. Одна из версий теоремы об униформации[англ.]* (принадлежащая Пуанкаре) утверждает, что любая риманова метрика на ориентированой замкнутой поверхности конформно эквивалентна по существу единственной метрике постоянной кривизны. Это даёт отправную точку к одному из подходов к теории Тейхмюллера, которая обеспечивает более тонкую классификацию римановых поверхностей, чем топологическая классификация лишь по эйлеровой характеристике.
Теорема об униформации[англ.]* утверждает, что любая риманова поверхность S комформно эквивалентна[англ.] поверхности, имеющей постоянную кривизну, которая может принимать значение 1, 0 или −1. Поверхность постоянной кривизны 1 локально изометрична сфере, что означает, что каждая точка поверхности имеет окрестность, изометричную открытому множеству на единичной сфере в с её внутренней римановой метрикой. Аналогично, поверхность постоянной кривизны 0 локально изометрична евклидовой плоскости, а поверхность постоянной кривизны −1 локально изометрична гиперболической плоскости.

Поверхности постоянной кривизны являются двухмерными реализациями объектов, которые известны как пространственные формы. Они часто изучаются с точки зрения эрлангенской программы Феликса Клейна при помощи гладких групп автоморфизмов. Любая связная поверхность с трёхмерной группой изометрий является поверхностью постоянной кривизны.
Комплексная поверхность — это комплексное два-многообразие а потому, является вещественным четыре-многообразием. Это не поверхность в смысле этой статьи.
История поверхностей
Отдельные свойства поверхностей вращения были известны ещё Архимеду. Развитие математического анализа в семнадцатом веке обеспечило более систематические подходы к их доказательству. Кривизну поверхностей общего виде первым изучал Эйлер. В 1760 году[2] он доказал формулу для кривизны поверхности, а в 1771 году[3] он рассматривал поверхности, заданные в параметрической форме. Монж изложил основы его теории в классическом труде L'application de l'analyse à la géometrie, который появился в 1795 году. Определяющий вклад в теорию поверхностей сделал Гаусс в двух выдающихся статьях, написанных в 1825 и 1827 годах[1]. Они наметили новую линию, отличную от традиционной, поскольку впервые Гаусс рассматривал внутреннюю геометрию поверхности, свойства, которые определяются лишь геодезическими расстояниями между точками на поверхности независимо от способа, которым поверхность расположена в окружающем евклидовом пространстве. Завершающим результатом является Theorema Egregium Гаусса, устанавливающая, что кривизна Гаусса является внутренним инвариантом, то есть инвариантом относительно локальных изометрий. Эту точку зрения распространил на пространства высоких размерностей Риман и основал то, что сейчас называется римановой геометрией. Девятнадцатый век был золотым веком теории поверхностей как с топологической, так и дифференциально-геометрической тoчки зрения, в котором многие ведущие геометры посвящали себя их изучению. Дарбу собрал много результатов в своём четырёхтомном трактате Théorie des surfaces (Теория поверхностей, 1887–1896).
Представленное ниже большей частью следует Гауссу, но с важными дополнениями от других геометров. В то время Гаусс был у Георга III картографом Великобритании и Ганновера. Это королевское покровительство может объяснить, почему эти работы содержат практические вычисления кривизны земли чисто на основе измерений на поверхности планеты.
Кривизна поверхности в евклидовом пространстве


Неформально Гаусс определяет кривизну поверхности в терминах кривизны некоторых плоских кривых, связанных с поверхностью. Он позднее нашёл серию эквивалентных определений. Одно из первых было сформулировано в терминах свойств отображения Гаусса, отображения из поверхности в 2-мерную сферу. Однако, до получения более естественного определения в терминах площади углов малых треугольников, Гауссу потребовалось осуществить глубокое исследование свойств геодезической на поверхности, то есть путей кратчайшей длины между двумя фиксированными точками на поверхности (см. ниже).[a]
Гауссова кривизна в точке на вложенной гладкой поверхности, заданной локально уравнением
в евклидовом пространстве (), определяется как произведение главных кривизн в точке[4]. Средняя кривизна определяется как их среднее. Главные кривизны — это максимальная и минимальная кривизны плоских кривых, полученных путём пересечения поверхности с плоскостями, перпендикулярными касательной плоскости в точке. Если точкой является (0, 0, 0) с касательной плоскостью , то, после вращения вокруг оси z и обнуления коэффициента при xy, F будет иметь разложение в ряд Тейлора
Главными кривизнами являются и . В этом случае гауссова кривизна задаётся формулой
а средняя кривизна формулой
Поскольку и являются инвариантами относительно изометрий , в общем случае
и
где производные в точке вычисляются по формулам[5]
Для любой ориентированной вложенной поверхности отображение Гаусса является отображением в единичную сферу, отображающим каждую точку в (направленный наружу) единичный нормальный вектор к ориентированной касательной плоскости в точке. В системе координат отображение отображает точку в
Прямые вычисления показывают, что гауссова кривизна является якобианом отображения Гаусса[6].
Примеры

Поверхности вращения
Поверхность вращения может быть получена вращением кривой в плоскости xz вокруг оси z в предположении, что кривая не пересекает ось z. Предположим, что кривая задана выражением
с t лежащим в (a, b), и параметризованная длиной дуги, так что
Тогда поверхность вращения является множеством точек
Гауссова кривизна и средняя кривизна задаются выражениями[7]

Геодезические на поверхности вращение определяются отношением Клеро[англ.].
Поверхность второго порядка
Рассмотрим поверхность второго порядка, заданную выражением[8]
Эта поверхность позволяет параметризацию
Гауссова кривизна и средняя кривизна задаются выражением

Линейчатые поверхности
Линейчатая поверхность является поверхностью, которая может быть получена движением прямой линии в [9][10]. Выбрав директрису на поверхности, то есть гладкую кривую единичной скорости c(t), ортогональную прямым, а затем выбрав как единичные вектора вдоль кривой в направлении прямых, для вектора скорости и u выполняется
Поверхность состоит из точек
при изменении s и t.
Тогда, если
гауссова и средняя кривизна задаются выражениями
Гауссова кривизна линейчатой поверхности обращается в нуль тогда и только тогда, когда и v пропорциональны[11]. Это условие эквивалентно тому, что поверхность является огибающей плоскостей вдоль кривой, содержащей касательный вектор v и ортогональный вектор u, то есть поверхность является развёртывающейся вдоль кривой[12]. Более обще поверхность в имеет нулевую гауссову кривизну близ точки тогда и только тогда, когда она развёртывается вблизи этой точки[13] (Эквивалентное условие даётся ниже в терминах метрики.)
Минимальные поверхности
В 1760 году Лагранж распространил результаты Эйлера вариационного исчисление с интегралами от одной переменной на интегралы от двух переменных[14][15]. Он обдумывал следующую задачу:
Если дана замкнутая кривая в , находим поверхность минимальной площади, имеющая кривую в качестве границы.
Такая поверхность называется минимальной поверхностью.
В 1776 году Жан Батист Мёнье показал, что дифференциальное уравнение, полученное Лагранжем, эквивалентно обращению в нуль средней кривизны поверхности:
Поверхность минимальна тогда и только тогда, когда средняя кривизна обращается в нуль.
Минимальные поверхности имеют простую интерпретацию в реальной жизни — они имеют форму мыльной плёнки, если проволочную рамку окунуть в мыльный раствор и осторожно вынуть. Вопрос, существует ли минимальная поверхность с заданной границей, называется задачей Плато по имени бельгийского физика Жозефа Плато, который проводил эксперименты с мыльными плёнками в середине девятнадцатого века. В 1930 году Джесси Дуглас и Тибор Радо дали положительный ответ на задачу Плато (Дуглас получил одну из первых филдсовских премий за эту работу в 1936 году)[16].
Известно много примеров минимальных поверхностей, такие как катеноид, геликоид, поверхность Шерка?! и поверхность Эннепера. В этой области проводились интенсивные исследования, итог которых подведён в книге Оссермана[17]. В частности, результат Оссермана показывает, что если минимальная поверхность не планарна, то её образ при отображении Гаусса плотен в .

Поверхности постоянной гауссовой кривизны

Если поверхность имеет постоянную гауссову кривизну, она называется поверхностью постоянной кривизны[18][19][20].
- Единичная сфера в имеет постоянную гауссову кривизну +1.
- Евклидова плоскость и цилиндр имеют постоянную гауссову кривизну 0.
- Поверхность вращения с имеет постоянную гауссову кривизну –1. Частный случай получается путём принятия , и [19][21][22]. Последний случай является классической псевдосферой, образованной вращением трактрисы вокруг центральной оси. В 1868 году Эудженио Бельтрами показал, что геометрия псеводосферы была напрямую связана с геометрией гиперболической плоскости, открытой независимо Лобачевским (1830) и Бойяи (1832). Уже в 1840 году Ф. Майндинг, студент Гаусса, получил тригонометрические формулы для псевдосферы, идентичные формулам для гиперболической плоскости[23]. Эта поверхность постоянной кривизны ныне лучше понимается в терминах метрики Пуанкаре на верхней полуплоскости или единичном круге и может быть описана другими моделями, такими как модель Кляйна или гиперболоидная модель, полученная рассмотрением двулистного гиперболоида в трёхмерном пространстве Минковского, где [24].
Каждая из этих поверхностей постоянной кривизны имеет транзитивную группу Ли симметрий. Этот теоретико-групповой факт имеет далеко идущие следствия, которые особенно замечательны ввиду центральной роли, которую играют эти специальные поверхности в геометрии поверхностей согласно теореме об униформации[англ.]* Пуанкаре (см. ниже).
Другие примеры поверхностей с гауссовой кривизной 0 включают конусы, развёртывающиеся поверхности касательных[англ.] и, более обще, любая развёртывающаяся поверхность.
Структура локальной метрики


Для любой поверхности, вложенной в евклидово пространство размерности 3 и выше, можно измерить длину кривой на поверхности, угол между двумя кривыми и площадь области на поверхности. Эта структура закодирована инфинитезимально в римановой метрике на поверхности через элементы линий и элементы площади. В девятнадцатом и в начале двадцатого века рассматривались только поверхности, вложенные в , а метрика задавалась как 2×2 положительно определённая матрица, гладко меняющаяся от точки к точке в локальной параметризации поверхности. Идея локальной параметризации и изменение координат были формализованы позднее через абстрактное понятие многообразия, топологического пространства, где гладкая структура[англ.] задана локальными картами на многообразии, в точности как планета Земля отображается атласами сегодня. Изменения координат между различными картами той же самой области должны быть гладкими. Как контурные линии в реальных картах кодируют изменения в высоте над уровнем моря, принимая во внимание локальные искажения земной поверхности при вычислении истинных расстояний, так и риманова метрика описывает расстояния и площади «в малом» в каждой локальной карте. В каждой локальной карте риманова метрика задаётся гладко 2×2 положительно определённой матрицей в каждой точке. Когда берутся различные карты, матрица преобразуется согласно матрице Якоби изменения координат. Многообразие тогда имеет структуру 2-мерного риманового многообразия.
Элементы линии и площади
При выборе локальной карты, например, путём проекции на плоскость , элемент линии ds и элемент площади dA могут быть записаны в терминах локальных координат
и
- .
Выражение называется первой фундаментальной формой[25].
Матрица
должна быть положительна определена и гладко зависит от x и y.
Аналогичным образом элементы линии и площади могут быть ассоциированы с любым абстрактным римановом 2-многообразии в локальном графике.
Вторая фундаментальная форма
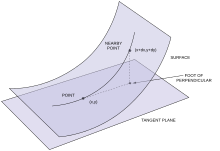
Внешняя геометрия поверхностей изучает свойства поверхностей, вложенных в евклидово пространство, обычно . Во внутренней геометрии две поверхности «одинаковы», если можно разогнуть одну поверхность в другую без растяжений, то есть образовать отображение одной поверхности в другую с сохранением расстояния. Так, цилиндр локально «одинаков» с плоскостью. Во внешней геометрии две поверхности «одинаковы», если они конгруэнтны в объемлющем евклидовом пространстве, то есть существует изометрия , переводящая одну поверхность в другую. С этим более жёстким определением одинаковости цилиндр и плоскость, очевидно, уже не одинаковы.
Хотя главными инвариантами при изучении внутренней геометрии поверхности являются метрика (первая фундаментальная форма) и гауссова кривизна, некоторые свойства поверхностей зависят также от вложения в (или в евклидово пространство большей размерности). Наиболее важным примером является вторая фундаментальная форма, которая классически определяется следующим образом[26][27][28].
Возьмём точку на поверхности в локальной карте. Евклидово расстояние от близкой точки до касательной плоскости в (x, y), то есть длина перпендикуляра, опущенного из этой точки на касательную плоскость имеет вид
плюс третья и более высокие поправки. Выражение выше, симметричная билинейная форма в каждой точке, является второй фундаментальной формой. Она описывается симметричной матрицей
которая зависит гладко от x и y. Гауссову кривизну можно вычислить как отношение определителей второй и третьей фундаментальаных форм:
Следует заметить, что Гаусс доказал, что она является внутренним инвариантом (см. его Theorema Egregium ниже).
Одним из других внешних численных инвариантов поверхности является средняя кривизна , определённая как сумма главных кривизн. Она задаётся формулой[25]
Коэффициенты первой и второй фундаментальных форм удовлетворяют определённым условиям совместимости, известным как уравнения Гаусса ― Кодацци. Они используют символы Кристоффеля , связанные с первой фундаментальной формой[29]:
Эти равенства могут также быть кратко выражены и выведены[англ.] на языке форм связности (согласно Эли Картану[30]). Пьер Бонне доказал, что две квадратичные формы, удовлетворяющие уравнениям Гаусса — Годацци, всегда однозначно определяют вложенную поверхность локально[31]. По этой причине уравнения Гаусса — Кодацци часто называют фундаментальными уравнениями для вложенных поверхностей, они точно определяют, откуда пришла внутренняя и внешняя кривизны. Они позволяют обобщения на поверхности, вложенные в более общие римановы многообразия.
Оператор формы

Дифференциал df отображения Гаусса f может быть использован для определения типа внешней кривизны, известной как оператор формы[32][33][34] или отображение Вейнгартена. Этот оператор первый раз появился явно в работе Вильгельма Бляшке и позднее явно в трактате Бурали-Форти и Бугатти[35]. Поскольку в каждой точке x поверхности касательное пространство является пространством со скалярным произведением, оператор формы можно определить как линейный оператор на этом пространстве фомйлой
для касательных векторов v, w (скалярное произведение имеет смысл, поскольку и w оба лежат в )[b]. Правая часть симметрична по v и w, так что оператор формы является самосопряжённым на касательном пространстве. Собственные значения являются главными кривизнами и в x. В частности, определитель оператора формы в точке является гуссовой кривизной, но он содержит также другую информацию, поскольку средняя кривизна является половиной следа оператора формы. Средняя кривизна является внешним инвариантом. Во внешней геометрии цилиндр является развёртывающимся, что означает, что любая часть его внутренне неразличима от части плоскости, поскольку его кривизна Гаусса одинаково обращается в нуль. Хотя, его средняя кривизна не равна нулю. Следовательно, внешне он отличается от плоскости.
В общем случае собственные вектора и значения оператора формы в каждой точке определяют направления, в которых поверхность изгибается в каждой точке. Собственные значения соответствуют главным кривизнам поверхности, а собственные вектора соответствуют главным направлениям. Главные направления задают направления, в которых вложенная в поверхность кривая должна идти, чтобы максимизировать или минимизировать кривизну.
Оператор формы задаётся в терминах компонент первой и второй фундаментальных форм уравнением Вейнгартена[англ.][36]:
Геодезические кривые на поверхности
Кривые на поверхности, которые имею минимальную длину между двумя точками, называются геодезическими. Это формы, которые принимает резинка, натянутая между двумя точками. Математически геодезические описываются с помощью дифференциального уравнения в частных производных из вариационного исчисления. Дифференциальная геометрия поверхностей вращается вокруг изучения геодезических. Остаётся открытым вопрос, любая ли риманова метрика на 2-мерной локальной карте возникает из вложения в 3-мерное евклидово пространство — теория геодезических обычно указывает, что это верно в важном случае, когда компоненты метрики являются аналитическими.
Геодезические
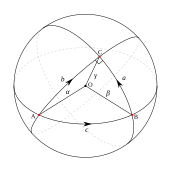
Если имеется кусочно гладкий путь в карте для t на [a, b], его длина определяется выражением
а энергия выражением
Длина не зависит от параметризации пути. Согласно уравнениям Эйлера — Лагранжа, если является путём, минимизирующим длину и параметризированным длиной дуги, он должен удовлетворять уравнениям Эйлера
где символы Кристоффеля задаются выражением
где и является матрицей, обратной . Путь, удовлетворяющий уравнениям Эйлера, называется геодезической. Согласно неравенству Коши — Буняковского минимизирующий энергию путь — это просто геодезическая, параметризованая длиной дуги, и для любой геодезической параметр t пропорционален длине дуги[4][24][37].
Геодезическая кривизна
Геодезическая кривизна в точке кривой , параметризованная длиной дуги, на ориентированной поверхности определяется выражением[38][39][40][41]
где является «главной» единичной нормалью к кривой на поверхности, построенной путём вращения единичного касательного вектора на угол +90°.
- Геодезическая кривизна в точке является внутренним инвариантом, зависящим только от метрики близ точки.
- Кривая единичной скорости на поверхности является геодезической тогда и только тогда, когда её геодезическая кривизна принимает значение нуль во всех точках на кривой.
- Кривая единичной скорости во вложенной поверхности является геодезической тогда и только тогда, когда её вектор ускорения нормален к поверхности.
Геодезическая кривизна измеряет точным образом как далека кривая на поверхности от геодезической.
Задача изометричного вложения
Результат Якобовича[42] и Позняка[43] показывает, что любая метрическая структура на поверхности возникает из локального вложения в . Помимо некоторых специальных случаев остаётся открытым вопрос, возможно ли это в , так называемая «проблема Вейля»[44]. В 1926 году Морис Жане доказал, что это всегда возможно локально, если E, F и G аналитичны. Вскоре после этого Эли Картан обобщил это на локальные вложения римановых n-многообразий в , где . Для доказательства теоремы Жане вблизи (0,0), теорема Коши — Ковалевской используется дважды для получения аналитических геодезических ортогональных оси y, а затем x, чтобы сделать аналитические изменения координат так, что и . Изометрическое вложение u должно удовлетворять
- .
Дифференцирование даёт три дополнительных равенства
- .
с заданными и . Эти уравнения можно решить около (0,0) с помощью теоремы Коши — Ковалевской и получить решение исходных уравнений вложения.

Ортогональные координаты
Когда в метрике, прямые, параллельные осям x и y, ортогональны и дают ортогональные координаты. Если , то гауссова кривизна задаётся выражением[13][45].
Если вдобавок , так что , то угол в точке пересечения между геодезической и прямой y = constant задаётся уравнениением
- Невозможно разобрать выражение (неизвестная функция «\tg»): {\displaystyle \tg \varphi = H\cdot \frac{\dot{y}}{\dot{x}}.}
Производная задаётся классической формулой Гаусса[13][4]:
Геодезические полярные координаты

Когда метрика на поверхности задана и базисная точка фиксирована, есть единственная геодезическая, соединяющая базисную точку с любой достаточно близкой точкой. Направление геодезической в базисной точке и расстояние единственным образом определяют другие точки. Эти две величины, направление и значение, тогда определяют касательный вектор в базисной точке. Отображение из касательных векторов к конечным точкам гладким образом заметают окрестность базисной точки и определяет так называемое «экспоненциальное отображение», которое определяет локальные координаты карты в базисной точке. Выметаемая окрестность имеет свойства, похожие на свойства шаров в евклидовом пространстве, а именно, любые две точки на ней связаны единственной геодезической. Такое свойство называется «геодезической кривизной», а координаты называются «нормальными координатами». Явное вычисление нормальных координат может быть выполнено путём рассмотрения дифференциального уравнения, соответствующего геодезическим. Свойства выпуклости являются следствием леммы Гаусса и её обобщений. Грубо говоря, эта лемма утверждает, что геодезические, начинающиеся в базисной точке, должны пересекать сферы фиксированного радиуса с центром в базисной точке под прямыми углами. Геодезические полярные координаты получаются при комбинации экспоненциального отображения с полярными координатами на касательных векторах в базисной точке. Гауссова кривизна поверхности тогда задаётся отклонением второго порядка метрики от евклидовой метрики. В частности, Гауссова кривизна является инвариантом метрики, знаменитая теорема Гаусса Theorema Egregium. Удобный способ понимания кривизны приходит из обыкновенных дифференциальных уравнений, которые первым рассматривал Гаусс, а затем обобщил Якоби. Эти уравнения возникают из изменения нормальных координат двух различных точек. Уравнение Гаусса — Якоби даёт другой способ вычисления гауссовой кривизны. Геометрически оно объясняет, что произойдёт с геодезическими из фиксированной базисной точки, когда конечная точка перемещается вдоль маленького сегмента кривой. Поведение геодезической показывается через данные, записанные в поле Якоби, векторном поле вдоль геодезической[46]. После одного с четвертью столетий после Гаусса и Якоби Марстон Морс дал более концептуальную интерпретацию поля Якоби в терминах второй производной функции энергии на бесконечномерном гильбертовом многообразии путей[37].
Экспоненциальное отображение
Теория обыкновенных дифференциальных уравнений показывает, что если гладкая, то дифференциальное уравнение с начальным условием имеет единственное решение для достаточно малых и это решение зависит гладко от t и . Из этого следует, что для достаточно малых касательных векторов v в заданной точке существует геодезическая , определённая на (−2,2) с и . Боле того, если , то . Экспоненциальное отображение задаётся выражением
- (1)
и даёт диффеоморфизм между кругом и окрестностью точки p. Более обще, отображение, переводящее (p,v) в , даёт локальный диффеоморфизм в окрестности (p,p). Экспоненциальное отображение даёт нормальные координаты вблизи p[24].
Вычисление нормальных координат
Существует стандартная техника (см, например, книгу Бергера[4]) для вычисления изменений переменных от нормальных координат u, v в точке как разложение в формальный ряд Тейлора. Если координаты x, y в (0,0) локально ортогональны, запишем
где L, M квадратичные, а , кубические однородные многочлены от u и v. Если u и v фиксированы, и могут рассматриваться как решения уравнений Эйлера в виде формальных степенных рядов — это единственным образом определяет , , , , и .
Лемма Гаусса

В этих координатах матрица g(x) удовлетворяет условию и прямые являются геодезическими через 0. Из равенства Эйлера вытекает матричное равенство
- ,
ключевой результат, обычно называемый леммой Гаусса. Геометрически она утверждает, что
геодезические через 0 пересека.т окружности с центром в 0 ортогонально.
Если взять полярные координаты , получаем, что метрика имеет вид
- .
В геодезических координатах легко проверить, что геодезические через нуль минимизируют длину. Топология на римановом многообразии задаётся функцией расстояния , а именно, нижней границей длин кусочногладких путей между p и q. Это расстояние реализуется геодезическими, так что в нормальных координатах . Если радиус достаточно мал, слегка усиленная лемма Гаусса показывает, что образ U диска при экспоненциальном отображении является геодезической кривизной, то есть любые две точки в U соединены единственной геодезической, лежащей полностью в U[47][48].
Theorema Egregium
Если координаты x и y поверхности в , соответствующие , разложение в степенной ряд метрики задаётся в нормальных координатах (u, v) как
Этот экстраординарный результат — гауссова Theorema Egregium — показывает, что гауссова кривизна поверхности может быть вычислена исключительно в терминах метрики, а потому является внутренним инвариантом поверхности, не зависящим от любого вложения в и не меняющемся при преобразовании координат. В частности, изометрии поверхностей сохраняют Гауссову кривизну[4].
Уравнение Гаусса — Якоби
Если взять изменение нормальных координат в точке p к нормальным координатам в близкой точке q, получаем уравнение Штурма — Лиувилля при , открытое Гауссом и позднее обобщенное Густавом Якоби,
Якобиан изменения этих координат в точке q равен . Это даёт другой способ определения внутренней природы гауссовой кривизны. Поскольку можно интерпретировать как длину элемента линии в направлении , уравнение Гаусса — Якоби показывает, что гауссова кривизна измеряет распространение геодезических на геометрической поверхности при удалении от точки[49].
Оператор Лапласа–Белтрами
На поверхности с локальной метрикой
и оператором Лапласа — Бельтрами|
где , гауссова кривизна в точке задаётся формулой[50]
где r обозначает геодезическое расстояние от точки. Поскольку является внутренним инвариантом, это даёт ещё одно доказательство, что гауссова кривизна является внутренним инвариантом.
В изотермической системе координат, которую первым рассматривал Гаусс, требуется, чтобы метрика была специального вида
В этом случае оператор Лапласа — Бельтрами задаётся выражением
и удовлетворяет уравнению Лиувилля[51]
Известно, что изотермические системы координат существуют в окрестности любой точки поверхности, хотя все проверки на сегодняшний день опираются на нетривиальные результаты из области дифференциальных уравнений в частных производных[52]. Существует элементарное доказательство для минимальной поверхности[53].
Теорема Гаусса — Бонне

На сфере или гиперболоиде площадь геодезического треугольника, то есть треугольника, все стороны которого являются геодезическими, пропорциональна разнице сумм внутренних углов с . Константа пропорциональности является просто гауссовой кривизной, постоянной для этих поверхностей. Для тора разность равна нулю, что отражает факт, что его гауссова кривизна равна нулю. Это стандартные результаты в сферической, гиперболической и высшей тригонометрии (см. ниже). Гаусс обобщил эти результаты на произвольные поверхности показав, что интеграл гауссовой кривизны по внутренности геодезического треугольника равен его угловой невязке (нехватке или избытке). Его формула показала, что гауссова кривизна может быть вычислена близ точки как предел площади по угловой невязке для геодезических треугольников, стягивающихся к точке. Поскольку любая замкнутая поверхность может быть разбита на геодезические треугольники, формула может быть использована для вычисления интеграла кривизны по всей поверхности. Как специальный случай того, что сейчас называется теоремой Гаусса — Бонне, Гаусс доказал, что этот интеграл всегда равен на целое число, топологический инвариант поверхности, называемый эйлеровой характеристикой. Этот инвариант легко вычисляется в терминах числа вершин, рёбер и граней треугольников в разбиении, которое называется триангуляцией. Эта связь анализа и топологии была предвестником многих более поздних результатов в геометрии, достигших апогея в теореме Атьи — Зингера об индексе. В частности, свойства кривизны накладывают ограничения на топологию поверхности.
Геодезические треугольники
Гаусс доказал, что кагда является геодезическим треугольником на поверхности с углами , и в вершинах A, B и C, то
Фактически, принимая геодезические полярные координаты в начале координат A и AB, AC радиусы с полярными углами 0 и :
где второе равенство вытекает из равенства Гаусса — Якоби, а четвёртое из формулы производной Гаусса в ортогональной системе координат .
Формула Гаусса показывает, что кривизна в точке может быть вычислена как предел угловой невязки по площади для всё более маленьких геодезических треугольников рядом с точкой. Качественно поверхность положительно или отрицательно выгнута согласно знаку угловой невязки для произвольно маленьких геодезических треугольников[25]
Теорема Гаусса — Бонне

Поскольку любое компактное ориентированное 2-многообразие M может быть триангулировано маленькими геодезическими треугольниками, отсюда следует, что
где означает эйлерову характеристику поверхности.
Фактически, если есть F граней, E рёбер и V вершин, то и левая часть равна .
Это знаменитая теорема Гаусса — Бонне. Она показывает, что интеграл гауссовой кривизны равен топологическому инварианту многообразия, а именно, эйлеровой характеристике. Эту теорему можно интерпретировать многими способами. Возможно, одной из наиболее далеко идущих интерепретаций служит теорема для эллиптического дифференциального оператора на M, один из простейших случаев теоремы Атьи — Зингера об индексе. Другой связанный результат, который может быть доказан с помощью теоремы Гаусса — Бонне, это теорема Пуанкаре о векторном поле для векторных полей на многообразии M, которые принимают значение ноль лишь на конечном числе точек — сумма индексов в этих точках равна эйлеровой характеристике, где индекс точки определяется следующим образом: на малой окружности вокруг изолированного нуля векторное поле определяет отображение в единичную окружность, индекс равен просто порядку точки этого отображения.) [25]
Кривизна и вложения
Если гауссова кривизна поверхности M везде положительна, то эйлерова характеристика положительна, так что M гомеоморфна (а потому и диффеоморфна) . Если вдобавок поверхность изометрично вложена в , отображение Гаусса обеспечивает явный диффеоморфизм. Как заметил Адамар, в этом случае поверхность выпукла. Этот критерий выпуклости можно рассматривать как двумерное обобщение хорошо известного критерия выпуклости плоской кривой по второй производной. Гильберт доказал, что любая изометрично вложенная замкнутая поверхность должна иметь точку с положительной кривизной. Таким образом, замкнутое риманово 2-многообразие неположительной кривизны никогда не может быть вложено изометрично в . Однако, как показал Адриано Гарсиа с помощью уравнения Бельтрами для квазикомформных отображений[англ.], это всегда возможно для некоторой кофмормной эквивалентности[англ.][54][55].
Поверхности постоянной кривизны
Односвязные поверхности постоянной кривизны 0, +1 и –1 это евклидова плоскость, единичная сфера в и гиперболическая плоскость. Каждая из них имеет транзитивную трёхмерную группу Ли сохраняющих ориентацию изометрий G, которая может быть использована для изучения геометрии поверхности. Каждая из двух некомпактных поверхностей может быть идентифицирована фактор-группой G / K, где K является максимальной компактной подгруппой группы G. Здесь K изоморфна SO(2). Любое другое замкнутое риманово 2-многообразие M постоянной гауссовой кривизны после умножения метрики на постоянную будет обязательно иметь одну из этих трёх поверхностей в качестве своего универсальное накрывающего пространства. В ориентированном случае фундаментальная группа многообразия M может быть отождествлена с однородной подгруппой без кручения группы G, а M может быть отождествлена с двойным смежным классом[англ.] . В случае сферы и евклидовой плоскости единственно возможными примерами являются сама сфера и тор, полученный как фактор-группа R2 по дискретным подгруппам ранга 2. Для замкнутых поверхностей рода , пространство модулей римановых поверхностей, полученных при пробегании по всем таким подгруппам, имеет вещественную размерность 6g − 6[56]. По теореме об униформации[англ.]* Пуанкаре, любое ориентированное замкнутое 2-многообразие комформно эквивалентно[англ.] поверхности постоянной кривизны 0, +1 или –1. Другими словами, при умножении метрики на положительную величину гауссова кривизна может быть приведена в точности к одному из этих значений (знаку эйлеровой характеристики многообразия M)[57][58].
Евклидова геометрия

В случае евклидовой плоскости группой симметрии является евклидова группа движений[англ.], полупрямое произведение двуменой группы параллельных переносов на группу вращений[59]. Геодезическими являются прямые и геометрия закодирована в элементарные формулы тригонометрии, такие как теорема косинусов для треугольника со сторонами a, b, c и углами , , :
Плоский тор может быть получен как фактор-группа на решётку, то есть свободную абелеву подгруппу ранга 2. Эти замкнутые поверхности не имеют изометрических вложений в . Тем не менее, они позволяют изометричные вложения в . В простейшем случае это следует из факта, что тор является произведением двух окружностей и может быть изометрично вложен в [60].
Сферическая геометрия


Группа изометрий единичной сферы в является ортогональной группой O(3) с группой вращений SO(3) в качестве подгруппы изометрий, сохраняющих ориентацию. Она является прямым произведением SO(3) на антиподальное отображение[англ.], переводящее x в –x[61]. Группа SO(3) действует транзитивно на . Подгруппа стабилизаторов единичного вектора (0,0,1) может быть отождествлено с SO(2), так что .
Геодезические между двумя точками на сфере являются дугами большого круга с этими заданными конечными точками. Если точки не антиподальны, существует единственная кратчайшая геодезическая между точками. Геодезические могут быть описаны также с помощью теории групп — каждая геодезическая через северный полюс (0,0,1) является орбитой подгруппы вращений вокруг оси, проходящей через две антиподальные точки экватора.
Сферический треугольник — это геодезический треугольник на сфере. Он определяется точками A, B и C на сфере со сторонами BC, CA и AB, образованными дугами больших окружностей с длиной, меньшей . Если длины сторон равны a, b и c, а углы между сторонами равны , и , то сферическая теорема косинусов утверждает, что
Площадь треугольника задаётся формулой
- .
Используя стереографическую проекцию из северного полюса сфера может быть отождествлена с расширенной комплексной плоскостью . Явное отображение задаётся выражением
При таком отображении любое вращение S2 соответствует преобразованию Мёбиуса в SU(2), единственному с точностью до знака[62]. По отношению к координатам (u, v) на комплексной плоскости сферическая метрика превращается в[63]
Единичная сфера является единственной замкнутой ориентированной поверхностью с постоянной кривизной +1. Фактор-группа SO(3)/O(2) может быть отождествлена с вещественной проективной плоскостью. Она не ориентирована и может быть описана как фактор-группа S2 на антподальное отображение (умножение на −1). Сфера односвязна, в то время как вещественная проективная плоскость имеет фундаментальную группу Z2. Конечные подгруппы SO(3), соответствующие конечным подгруппам O(2) и группам симметрии правильных многогранников, не действуют свободно на S2, так что соответствующие частные не являются 2-многообразиями, а лишь орбифолдами.
Гиперболическая геометрия

Неевклидова геометрия[64][65] впервые обсуждалась в письмах Гаусса, который выполнил большие вычисления на исходе девятнадцатого века и, хотя в частном порядке письма посылались, он решил их не публиковать. В 1830 году Лобачевский и, независимо, в 1832 году Бойяи, сын математика, переписывавшегося с Гауссом, опубликовали синтетические версии новой геометрии, за которые их сильно критиковали. Однако это продолжалось лишь до 1868 года, когда Белтрами, а вслед за ним Кляйн в 1871 и Пуанкаре в 1882, дали конкретные аналитические модели теории, которой Кляйн дал название гиперболическая геометрия. Было представлено четыре модели 2-мерной гиперболической геометрии
- Модель Бельтрами — Кляйна;
- Диск Пуанкаре;
- Верхняя полуплоскость Пуанкаре;
- Гиперболоидная модель Вильгельма Киллинга в трёхмерном пространстве Минковского.
Первая модель на основе диска имеет преимущество в том, что геодезические являются отрезками прямой (то есть, пересечениями евклидовых прямых с открытым единичным диском). Вторая модель имеет преимущество в том, что она даёт полную параллель с единичной сферой в 3-мерном евклидовом пространстве. Ввиду приложений в комплексном анализе и геометрии, однако, модели Пуанкаре употребляются наиболее часто. Модели взаимозаменяемы благодаря преобразованиям Мёбиуса между диском и верхней полуплоскостью.
Пусть
будет диском Пуанкаре на комплексной плоскости с метрикой Пуанкаре
В полярных координатах метрика задаётся выражением
Длина кривой задаётся формулой
Группа , заданная как
действует транзитивно посредством преобразований Мёбиуса на D, а стабилизатор подгруппы 0 является группой вращений
Факторгруппа SU(1,1)/±E является группой сохраняющих ориентацию изометрий круга D. Любые две точки z и w в D соединены единственной геодезической, которая представлена куском окружности или прямой, проходящих через z и w и ортогональных границе круга. Расстояние между z и w задаётся формулой
В частности и является геодезической через 0 вдоль вещественной оси, параметризованной длиной дуги.
Топология, определённая данной метрикой эквивлентна обычной евклидовой топологии, хотя как метрическое пространство (D,d) оно полно.

Гиперболический треугольник является геодезическим треугольником для этой метрики — любые три точки в D являются вершинами гиперболического треугольника. Если стороны имеют длины a, b и c с соответствующими углами , и , то гиперболическая теорема косинусов утверждает, что
Площадь гиперболического треугольника задаётся равенством[66]
- .
Единичный диск и верхняя полуплоскость
конформно эквивалентны по преобразованиям Мёбиуса
При таком отображении действие SL(2,R) преобразований Мёбиуса на H соответствует действию SU(1,1) на D. Метрика на H становится
Поскольку прямые или окружности сохраняются при преобразованиях Мёбиуса, геодезические снова описываются прямыми или окружностями, ортогональными вещественной оси.
Единичный диск с метрикой Пуанкаре является единственным односвязным ориентированным 2-мерным римановым многообразием с постоянной кривизной −1. Любая ориентированная замкнутая поверхность M с таким свойством имеет D в качестве универсального накрывающего пространства. Его фундаментальная группа может быть отождествлена с кокомпактной подгруппой без кручений группы SU(1,1) таким образом, что
В этом случае является конечно представимой группой. Образующие и отношения закодированы в геодезической кривизне фундаментального геодезического многоугольника[англ.] в D (или H), геометрически соответствующего замкнутой геодезической на M.
Примеры.
- Поверхность Больцы рода 2;
- Квартика Кляйна[англ.] рода 3;
- Поверхность Макбита рода 7;
- Первая тройка Гурвица[англ.] рода 14.
Теорема об униформации
Если дана ориентированная замкнутая поверхность M с гауссовой кривизной K, метрика на M может быть изменена конформно путём умножения её на множитель . Новая гауссова кривизна K′ тогда задаётся формулой
где является лапласианом исходной метрики. Тогда для того, чтобы показать, что заданная поверхность конформно эквивалентна метрике с постоянной кривизной , достаточно решить следующий вариант уравнения Лиувилля:
Если M имеет эйлерову характеристику 0, то она диффеоморфна тору, , так что это сводится к решению
Согласно стандартной эллиптической теории это возможно, поскольку интеграл K над M равен нулю по теореме Формула Гаусса — Бонне[67][68].
Когда M имеет отрицательную эйлерову характеристику, , так что уравнение принимает вид
Если использовать непрерывность экспоненциального отображения на пространстве Соболева, согласно Нейлу Трюдингеру это нелинейное уравнение может всегда быть решено[69][70].
Наконец, в случае 2-сферы, и уравнение превращается в
Хотя это нелинейное уравнение не решено прямо, из классических результатов, таких как теорема Римана — Роха, вытекает, что оно всегда имеет решение[71]. Метод потоков Риччи, разработанные Ричардом Гамильтоном, даёт другое доказательство существования на основе нелинейных дифференциальных уравнений в частных производных[72]. Фактически, поток Риччи на конформных метриках на определяется на функциях выражением
Чоу показал, что за конечное время K′ становится положительным. Отталкиваясь от предыдущих результатов, Гамильтона мог бы теперь показать, что K′ сходится к +1[73]. Ещё до этих результатов по потокам Риччи Осгуд, Филлипс и Сарнак[74] дали альтернативный и технически более простой подход к униформизации, основываясь на потоке на римановых метриках g, определённой выражением .
Простое доказательство, использующее только эллиптические операторы, открытое в 1988, можно найти в статье Динга[75]. Пусть G будет функцией Грина на , удовлетворяющая , где является точечной мерой в фиксированной точке P поверхности . Уравнение имеет гладкое решение v, поскольку правая сторона имеет интеграл 0 по теореме Гаусса — Бонне. Тогда удовлетворяет всегда на P. Отсюда следует, что является полной метрикой постоянной кривизны 0 на дополнении P, которая поэтому изометрична плоскости. В сочетании с стереографической проекцией из этого следует, что имеется гладкая функция u, такая что имеет гауссову кривизну +1 на компоненте P. Функция u автоматически расширяется до гладкой функции на всей .[c]
Поверхности неположительной кривизны
В области, где кривизна удовлетворяет , геодезические треугольники удовлетворяют CAT(0)[англ.] неравенству геометрии сравнения, которую изучали Картан, Александров и Топоногов, и рассматривали позже с другой точки зрения[англ.] Брюа[англ.] и Титс. Благодаря Громову это описание неположительной кривизны в терминах лежащего в основе метрического пространства имело глубокое влияние на современную геометрию и, в частности, на геометрические теории групп. Много результатов, известных для гладких поверхностей и их геодезических, такие как метод Биркгофа построения геодезических путём применения его процесса укорочения кривой или теорема Мангольдта и Адамара, что односвязная поверхность неположительной кривизны гомеоморфна плоскости, остаются верными для этих более общих условиях.
Неравенство сравнения Александрова

Простейший вид неравенства сравнения, впервые доказанного для поверхностей Александровым около 1940, утверждает, что
Расстояние между вершиной геодезического треугольника и средней точкой противоположной стороны всегда меньше, чем соответствующее расстояние в треугольнике сравнения на плоскости с теми же длинами сторон.
Неравенство следует из факта, что если c(t) описывает геодезическую, параметризованную длиной дуги, а a является фиксированной точкой, то
является выпуклой функцией, то есть
Если взять геодезические полярные координаты с началом в a так, что , выпуклость эквивалентна
При переходе к нормальным координатам u, v на c(t) это неравенство превращается в
- ,
где соответствует единичному вектору . Это следует из неравенства , следствие неотрицательности производной от вронскиана от H и r в теории Штурма — Лиувилля[4][77].

Существование геодезических
На полной кривой поверхности любые две точки могут быть соединены геодезической. Это частный случай теоремы Хопфа — Ринова, которая также применима в более высоких размерностях. Предположение полноты автоматически выполняется для поверхности, которая вложена как замкнутое подмножество евклидова пространства. Однако, это больше не выполняется, если, например, мы удаляем изолированную точку с поверхности. Например, дополнение начала координат из евклидовой плоскости является примером неполной поверхности. В этом примере две точки, диаметрально противоположные относительно начала координат не могут быть соединены геодезической без покидания плоскости без точки.
Теорема Мангольдта — Адамара
Для замкнутых поверхностей неположительной кривизны фон Мангольдт (1881) и Адамар (1898) доказали, что экспоненциальное отображение в точке является накрывающим, так что универсальным накрывающим пространством многообразия является . Этот результат обобщил на более высокие размерности Картан и обычно упоминается этот результат как Теорема Адамара — Картана. Для поверхностей этот результат следует из трёх важных фактов[60][4]
- Экспоненциальное отображение имеет ненулевой якобиан везде для поверхностей с отрицательной кривизной, следствие необращения в нуль .
- Любая геодезическая является бесконечно продолжаемой, результат, известный как Теорема Хопфа — Ринова для n-мерных многообразий. В двухмерном случае, если геодезическая стремится к бесконечности в направлении точки x, замкнутый диск D с центром в близкой точке y с удалённой x может быть стянут в y вдоль геодезической, что топологически невозможно.
- Любые две точки в классе гомотопии связаны единственной геодезической (см. выше).
Риманова связность и параллельный перенос

Классический подход Гаусса к дифференциальной геометрии поверхностей был стандартным элементарным подходом[13][78][4][24], который предшествовал появлению концепций римановых многообразий, предложенных Бернхардом Риманом в середине девятнадцатого века и связности, разработанной Туллио Леви-Чивита, Эли Картаном и Германом Вейлем в начале двадцатого века. Понятие связности, ковариантной производной и параллельного переноса дали более концептуальный и единообразный путь понимания кривизны, который не только позволил обобщения на многообразия более высоких размерностей, но и дал важное средство для определения новых геометрических инвариантов, называемых характеристическимм классами[79]. Подходы, использующие ковариантные производные и связность были использованы в более современных книгах[60][80][54].
Ковариантная производная
Связность поверхности можно определить различными эквивалентными путями, но с одинаково важными точками зрения. Связность Римана или связность Леви-Чивиты[25] проще всего понять в терминах поднятия векторных полей, рассматриваемых как дифференциальные операторы первого порядка, действующих на функциях на многообразиях, к дифференциальным операторам на касательном расслоении или расслоении реперов[англ.]. В случае вложенной поверхности подъём до оператора на векторных полях, называемый ковариантной производной, очень просто описывается в терминаз ортогональной проекции. Более того, векторное поле на поверхности, вложенной в , может пониматься как функция из поверхности в . Другое векторное поле действует как оператор дифференцирования покомпонентно. Получающееся векторное поле не будет касательным к поверхности, но это можно исправить, взяв ортогональную проекцию в касательное пространство в каждой точке поверхности. Риччи и Леви-Чивита осознали на исходе двадцатого века, что этот процесс зависит только от метрики и может быть локально выражен в терминах символов Кристоффеля.

Параллельный перенос
Параллельный перенос касательных векторов вдоль кривой на поверхности был следующим важным шагом вперёд благодаря Леви-Чивита [25]. Он связан с более ранним понятием ковариантной производной, поскольку является монодромией обыкновенного дифференциального уравнения на кривой, определённой ковариантной производной с учётом скорости вектора кривой. Параллельный перенос вдоль геодезических, «прямых» на плоскости, может также просто описан прямо. Вектор в касательной плоскости переносится вдоль геодезической как единственное векторное поле с постоянной длиной и имеющих постоянный угол со скоростью вектора геодезической. Для кривой общего вида этот процесс следует модифицировать с помощью геодезической кривизны, которая измеряет как далеко кривая отходит от геодезической[4]
Векторное поле вдоль кривой единичной скорости , с геодезической кривизной , говорят, что параллельно вдоль кривой, если
- оно имеет постоянную длину
- угол , которое оно имеет с вектором скорости , удовлетворяет уравнению
Это возвращает правило параллельного переноса вдоль геодезической или кусочно геодезической кривой, поскольку в этом случае , так что угол остаётся постоянной на любом отрезке геодезической. Существование параллельного переноса следует из того, что может быт вычислена как интеграл геодезической кривизны. Поскольку это зависит непрерывно от нормы , отсюда следует, что параллельный перенос для произвольной кривой может быть получен как предел параллельного переноса на приближении кусочно-геодезических кривых[81][82].
Связь может быть тогда описана в терминах поднятия путей в многообразии к путям в касательном или ортогональном расслоении реперов, что формализует классическую теорию "подвижного репера[83]. Подъём петель вокруг точки приводит к группе голономии в этой точке. Гауссова кривизна в точке может быть извлечена из параллельного переноса вокруг убывающих петель в точке. Эквивалентно кривизна может быть вычислена прямо на инфинитезимальном уровне в терминах скобок Ли[англ.] поднятых векторных полей.

1-форма связности
Подход Картана и Вейля, использующий 1-формы связности на расслоении реперов[англ.] поверхнсти M, даёт третий путь для понимания римановой связности. Они заметили, что параллельный перенос требует, чтобы путь на поверхности был поднят до пути в расслоении реперов так, что его касательные вектора лежат в специальном подпространстве коразмерности единица в трёхмерном касательном пространстве расслоения реперов. Проекция в это подпространство определяется дифференциальной 1-формой на ортонормальном расслоении реперов, формой связности. Это позволяет закодировать свойства кривизны в дифференциальных формах на расслоении реперов и формулы, вовлекающих их дифференциальные формы.
Этот подход особенно прост для вложенной поверхности. Согласно результату Кобаяши[84] 1-форма связности на поверхности, вложенной в евклидово пространство является просто обратным образом отображения Гаусса 1-формы связности на [85]. Использование отождествление с однородным пространством , 1-форм связности является просто компонентой 1-формы Маурера-Картана на SO(3)[86].
Глобальная дифференциальная геометрия поверхностей
Хотя описание кривизны использует только локальную геометрию поверхности, имеются важные глобальные аспекты, такие как теорема Гаусса — Бонне, теоремы об униформации[англ.]*, теорема Мангольдта — Адамара и теорема вложенности. Есть другие важные аспекты глобальной геометрии поверхностей[87][60][88][89]. Они включают:
- Радиус инъективности, определённый как наибольший r, такой что две точки на расстоянии, меньшим r, соединены единственной геодезической. Вильгельм Клингенберг доказал в 1959 году, что радиус инъективности замкнутой поверхности ограничен снизу минимумом из и длины наименьшей замкнутой геодезической. Это уточнённая теорема Бонне, который показал в 1855 году, что диаметр замкнутой поверхности положительной гауссовой кривизны всегда ограничен сверху величиной . Другими словами, геодезическая реализующая метрическое расстояние между двумя точками не может иметь длину больше, чем .
- Жёсткость. В 1927 году Кон-Фоссен доказал, что два изометричных овалоида – замкнутые поверхности с положительной гауссовой кривизной – обязательно конгруэнтны по изометрии . Однако, замкнутая вложенная поверхность с положительной гауссовой кривизной и постоянной средней кривизной обязательно является сферой. Аналогично, замкнутая вложенная поверхность постоянной гауссовой кривизны должна быть сферой (Либман, 1899). Хайнц Хопф показал в 1950 году, что замкнутая вложенная поверхность с постоянной средней кривизной и родом 0, то есть гомеоморфная сфере, обязательно является сферой. Пятью годами позже Александров удалил топологическое предположение. В 1980-х годах Венте построил погруженный тор постоянной средней кривизны в евклидово 3-пространство.
- Гипотеза Каратеодори: Гипотеза утверждает, что замкнутая выпуклая три раза дифференцируемая поверхность допускает по меньшей мере две точки округления. Первой работой по этой гипотезе была работа Ганса Гамбургера в 1924, который заметил, что гипотеза следует из следующего более строгого утверждения: Полуцелый индекс расслоения главной кривизны изолированной омбилики не превосходит единицы.
- Нулевая гауссова кривизна: полная поверхность в с нулевой гауссовой кривизной должна быть цилиндром или плоскостью.
- Теорема Гильберта (1901): никакая полная поверхность с постоянной отрицательной кривизной не может быть погружена изометрично .

- гипотеза Вилмора[англ.]. Эта гипотеза утверждает, что интеграл от квадрата средней кривизны тора, вложенного в , должен быть ограничен снизу величиной . Известно, что интеграл является инвариантом Мёбиуса. Гипотезу решили в 2012 Фернандо Кода Маркес и Андрк Невес[90].
- Изопериметрическая неравенства. В 1939 Шмидт доказал, что классическое изопериметрическое неравенство для кривых на евклидовой плоскости также верно на сфере или на гиперболической плоскости. А именно, он доказал, что среди всех замкнутых кривых, ограничивающих область фиксированной площади, периметр минимален, если кривая является окружностью в этой метрике. В размерности на единицу больше, известно, что среди всех замкнутых поверхностей в , возникающих как граница ограниченной области единичного объёма, площадь поверхности минимально у евклидова шара.
- Систолические неравенства для кривых на поверхностях[англ.]*. Если дана замкнутая поверхность, её систола[англ.] определяется как наименьшая длина любой не стягиваемой в точку кривой на поверхности. В 1949 году Лёвнер доказал неравенство тора[англ.] для метрик на торе, а именно, что площадь тора, делённая на квадрат его систолы, ограничена снизу величиной с равенством в случае постоянной кривизны. Аналогичный результат даётся неравенством Пу для вещественной проективной плоскости 1952 года с нижней границей , также достижимой в случае постоянной кривизны. Для бутылки Клейна, Блаттер и Бавард позднее получили нижнюю границу . Для замкнутой поверхности рода g, Хебда и Бугаро показали, что отношение ограничено снизу величиной . Тремя годами позднее Михаил Громов нашёл нижнюю границу, которая с точностью до постоянного множителя равна , хотя она не оптимальна. Асимптотически строгие верхняя и нижняя границы равны с точностью до постоянного множителя . Границы нашли Громов и Бузер-Сарнак, их можно найти в статье Катца[91]. Имеется также версия для метрики на сфере, в которой для систолы берётся длина наименьшей по длине замкнутой геодезической. Громов высказал гипотезу о нижней границе в 1980 году, лучшим результатом на настоящее время является нижняя граница , полученная Региной Ротман в 2006 году[92].
Что читать далее
Одним из наиболее обширных вводных обзоров по теме с описанием истории развития от догауссовского периода до современности принадлежит Бергеру[4]. Рассмотрение классической теории дано в книгах Айзенхарта[13], Крейзига[78] и Штрука[93]. Более современные одинаково иллюстрированные книги для студентов Грея, Аббен м Саламона[22], Пресли[94] и Вильсона[24] могут быть более доступными. Достаточное количество классической теории можно найти в книге Гильберта и Кон-Воссена[20]. Более сложные обсуждения студенческого уровня с использованием римановой связности на поверхности[англ.] можно найти в статьях Сингера и Торпа[54], до Кармо[60] и О’Нила[80].
См. также
Примечания
- ↑ Это конечное положение резинки, натянутой между двумя фиксированными точками на поверхности.
- ↑ Заметим, что в некоторых более свежих текстах симметричная билинейная форма в правой части называется второй фундаментальной формой, однако это не соответствует классическому определению второй фундаментальной формы.
- ↑ Это следует из аргументов, вовлекающих теорему Сакса и Уленбека[76] об устранимых особенностях гармоничных отображений[англ.] конечной энергии.
- ↑ 1 2 Gauss, 1902.
- ↑ Euler, 1760.
- ↑ Euler, 1771.
- ↑ 1 2 3 4 5 6 7 8 9 10 Berger, 2004.
- ↑ Eisenhart, 2004, с. 123.
- ↑ Singer, Thorpe, 1967, с. 223.
- ↑ do Carmo, 1976, с. 161–162.
- ↑ Eisenhart, 2004, с. 228–229.
- ↑ Eisenhart, 2004, с. 241–250.
- ↑ do Carmo, 1976, с. 188–197.
- ↑ do Carmo, 1976, с. 194.
- ↑ Eisenhart, 2004, с. 61–65.
- ↑ 1 2 3 4 5 Eisenhart, 2004.
- ↑ Eisenhart, 2004, с. 250–269.
- ↑ do Carmo, 1976, с. 197–213.
- ↑ Решение Дугласа описано в статье Куранта ((Courant 1950)).
- ↑ Osserman, 2002.
- ↑ Eisenhart, 2004, с. 270–291.
- ↑ 1 2 O'Neill, 1997, с. 249–251.
- ↑ 1 2 Hilbert, Cohn-Vossen, 1952.
- ↑ do Carmo, 1976, с. 168–170.
- ↑ 1 2 Gray, Abbena, Salamon, 2006.
- ↑ Stillwell, 1996, с. 1–5.
- ↑ 1 2 3 4 5 Wilson, 2008.
- ↑ 1 2 3 4 5 6 Levi-Civita, 1917.
- ↑ Eisenhart, 2004, с. 114–115.
- ↑ Pressley, 2001, с. 123–124.
- ↑ Wilson, 2008, с. 123–124.
- ↑ Eisenhart, 2004, с. 156.
- ↑ O'Neill, 1997, с. 257.
- ↑ do Carmo, 1976, с. 309–314.
- ↑ O'Neill, 1997, с. 195–216.
- ↑ do Carmo, 1976, с. 134–153.
- ↑ Singer, Thorpe, 1967, с. 216–224.
- ↑ Gray, Abbena, Salamon, 2006, с. 386.
- ↑ Gray, Abbena, Salamon, 2006, с. 394.
- ↑ 1 2 Milnor, 1963.
- ↑ Eisenhart, 2002, с. 131.
- ↑ Berger, 2004, с. 39.
- ↑ do Carmo, 1976, с. 248.
- ↑ O'Neill, 1997, с. 237.
- ↑ Jacobowitz, 1972.
- ↑ Poznjak, 1973.
- ↑ Han, Hong, 2006.
- ↑ Taylor, 1996a, с. Appendix C.
- ↑ doCarmo, 1976, с. 357.
- ↑ Berger, 2004".
- ↑ do Carmo, 1976, с. 303–305.
- ↑ O'Neill, 1997, с. 395.
- ↑ Helgason, 1978, с. 92.
- ↑ O'Niell, 1997, с. 286.
- ↑ do Carmo, 1976, с. 227.
- ↑ Osserman, 2002, с. 31–32.
- ↑ 1 2 3 Singer, Thorpe, 1967.
- ↑ Garsia, 1961, с. 93–110.
- ↑ Imayoshi, Taniguchi, 1992, с. 47–49.
- ↑ Berger, 1977.
- ↑ Taylor, 1996.
- ↑ Wilson, 2008, с. 1–23, Chapter I, Euclidean geometry.
- ↑ 1 2 3 4 5 do Carmo, 1976.
- ↑ Wilson, 2008, с. 25–49, Chapter II, Spherical geometry.
- ↑ Wilson, 2008, с. Chapter 2.
- ↑ Eisenhart, 2004, с. 110.
- ↑ Stillwell, 1990.
- ↑ Bonola, Carslaw, Enriques, 1955.
- ↑ Wilson, 2008, с. Chapter 5.
- ↑ Taylor, 1996b, с. 107.
- ↑ Berger, 1977, с. 341–343.
- ↑ Berger, 1977, с. 222–225.
- ↑ Taylor, 1996b, с. 101–108.
- ↑ Taylor, 1996b.
- ↑ Chow, 1991.
- ↑ Чен, Лу и Тянь (Chen, Lu, Tian 2006) указали на отсутствующий шаг в подходе Гамильтона и Чоу и подправили их подход. См. статью Эндрюса и Брайана (Andrews & Bryan 2009).
- ↑ Osgood, Phillips, Sarnak, 1988.
- ↑ Ding, 2001.
- ↑ Sacks, Uhlenbeck, 1981.
- ↑ Jost, 1997.
- ↑ 1 2 Kreyszig, 1991.
- ↑ Kobayashi, Nomizu, 1969, с. Chapter XII.
- ↑ 1 2 O'Neill, 1997.
- ↑ Arnold, 1989, с. 301–306, Appendix I..
- ↑ Berger, 2004, с. 263–264.
- ↑ Darboux, 1887-96.
- ↑ Kobayashi, 1956.
- ↑ Kobayashi, Nomizu, 1969.
- ↑ Ivey, Landsberg, 2003.
- ↑ Berger, 2004, с. 145–161.
- ↑ Chern, 1967.
- ↑ Hopf, 1989.
- ↑ Codá Marques, 2014, с. 683–782.
- ↑ Katz, 2007.
- ↑ Rotman, 2006, с. 3041-3047.
- ↑ Struik, 1988.
- ↑ Pressley, 2001.
Литература
- Fernando Codá Marques, André Neves. Min-Max theory and the Willmore conjecture // Annals of Mathematics. — 2014. — Т. 179, вып. 2. — doi:10.4007/annals.2014.179.2.6. — arXiv:1202.6036. — .
- Rotman R. The length of a shortest closed геодезической and the area of a 2-dimensional sphere // Proc. Amer. Math. Soc.. — 2006. — Вып. 134.
- Adriano M. Garsia. An imbedding of closed Riemann surfaces in Euclidean space // Comment. Math. Helv.. — 1961. — Т. 35. — С. 93–110. — doi:10.1007/BF02567009.
- Jürgen Jost. Nonpositive curvature: geometric and analytic aspects. — Birkhäuser, 1997. — (Lectures in Mathematics, ETH Zurich). — ISBN 978-0-8176-5736-9.
- Aleksandrov A.D., Zalgaller V.A. Instrinsic Geometry of Surfaces. — American Mathematical Society, 1967. — Т. 15. — (Translations of Mathematical Monographs).
- Оригинал А. Д. Александров, В. А. Залгаллер. Двумерные многообразия ограниченной кривизны (Основы внутренней геометрии поверхностей). — 1962. — Т. 63. — С. 3–262. — (Тр. МИАН СССР).
- Ben Andrews, Paul Bryan. Curvature bounds by isoperimetric comparison for normalized Ricci flow on the two-sphere // Calc. Var. Partial Differential Equations. — 2010. — Т. 39, вып. 3–4. — С. 419–428. — doi:10.1007/s00526-010-0315-5. — arXiv:0908.3606.
- Arnold V.I. Mathematical methods of classical mechanics. — 2nd. — New York: Springer-Verlag, 1989. — Т. 60. — (Graduate Texts in Mathematics). — ISBN 978-0-387-90314-9.
- оригинал Арнольд В.И. Математические методы классической механики. — 1974. — ISBN 5-354-00341-5.
- Marcel Berger. A Panoramic View of Riemannian Geometry. — Springer-Verlag, 2004. — ISBN 978-3-540-65317-2.
- Melvyn S. Berger. Nonlinearity and Functional Analysis. — Academic Press, 1977. — ISBN 978-0-12-090350-4.
- Roberto Bonola, Carslaw H. S., Enriques F. Non-Euclidean Geometry: A Critical and Historical Study of Its Development. — Dover, 1955. — ISBN 978-0-486-60027-7.
- см. также Роберто Бонола. Неевклидова геометрия (Критико-историческое изследованiе ея развитiя. — С.-Петербургъ, 1910.
- Simon Brendle. Ricci flow and the sphere theorem. — American Mathematical Society, 2010. — Т. 111. — (Graduate Studies in Mathematics). — ISBN 978-0-8218-4938-5.
- Élie Cartan. Geometry of Riemannian Spaces. — Math Sci Press, 1983. — ISBN 978-0-915692-34-7.; Перевод второго издания книги Leçons sur la géométrie des espaces de Riemann (1951).
- перевод Э. Катан. Геометрия римановых пространств. — Ленинград: ОНТИ НКТЦ СССР, 1936.
- Élie Cartan. Riemannian Geometry in an Orthogonal Frame (from lectures delivered by É Cartan at the Sorbonne in 1926-27). — World Scientific, 2001. — ISBN 978-981-02-4746-1..
- Xiuxiong Chen, Peng Lu, Gang Tian. A note on uniformization of Riemann surfaces by Ricci flow // Proc. AMS. — 2006. — Т. 134, вып. 11. — С. 3391–3393. — doi:10.1090/S0002-9939-06-08360-2.
- Chern S. S. Curves and Surfaces in Euclidean Spaces. — Mathematical Association of America, 1967. — (MAA Studies in Mathematics).
- Chow B. The Ricci flow on a 2-sphere // J. Diff. Geom.. — 1991. — Т. 33, вып. 2. — С. 325–334. — doi:10.4310/jdg/1214446319.
- Richard Courant. Dirichlet's Principle, Conformal Mapping and Minimal Surfaces. — John Wiley & Sons, 1950. — ISBN 978-0-486-44552-6.
- перевод Р. Курант. Принцип Дирихле, конформные отображения и минимальные поверхности. — Москва: издательство иностранной литературы, 1953.
- Gaston Darboux. Leçons sur la théorie générale des surfaces. — Gauthier-Villars, 1887-96. Том I (1887), Том II (1915) [1889], Том III (1894), Volume IV (1896).
- перевод Жан Гастон Дарбу. Лекции по общей теории поверхностей и геометрические приложения анализа бесконечно малых. — Москва, Ижевск, 2013. т1: isbn=978-5-4344-0118-0 т2: isbn=978-5-4344-0119-7 т3: isbn=978-5-4344-0120-3, т4 isbn=978-5-4344-0121-0
- Ding W. A proof of the uniformization theorem on S2 // J. Partial Differential Equations. — 2001. — Т. 14. — С. 247–250.
- Manfredo P. do Carmo. Differential Geometry of Curves and Surfaces. — Prentice-Hall, 1976. — ISBN 978-0-13-212589-5.
- перевод Манфредо до Кармо. Дифференциальная геометрия кривых и поверхностей. — Москва, Ижевск, 2013. — ISBN 978-5-4344-0150-0.
- Luther P. Eisenhart. A Treatise on the Differential Geometry of Curves and Surfaces. — Dover, 2004. — ISBN 978-0-486-43820-7. Full 1909 text
- Luther P. Eisenhart. An Introduction to Differential Geometry with Use of the Tensor Calculus. — Princeton University Press, 1947. — Т. 3. — (Princeton Mathematical Series). — ISBN 978-1-4437-2293-3.
- Recherches sur la courbure des surfaces // Mémoires de l'Académie des Sciences de Berlin. — 1760. — Т. 16. — С. 119–143.. Дата публикации - 1767
- Leonhard Euler. De solidis quorum superficiem in planum explicare licet // Novi Commentarii Academiae Scientiarum Petropolitanae. — 1771. — Т. 16. — С. 3–34.. Дата публикации - 1772
- Carl Friedrich Gauss. General Investigations of Curved Surfaces of 1825 and 1827. — Princeton University Library, 1902.
- Carl Friedrich Gauss. General Investigations of Curved Surfaces. — Hewlett, NY: Raven Press, 1965.
- Carl Friedrich Gauss. General Investigations of Curved Surfaces. — Mineola, NY: Dover Publications, 2005. — ISBN 978-0-486-44645-5.
- Alfred Gray, Elsa Abbena, Simon Salamon. Modern Differential Geometry of Curves And Surfaces With Mathematica. — CRC Press, 2006. — ISBN 978-1-58488-448-4.
- Qing Han, Jia-Xing Hong. Isometric Embedding of Riemannian Manifolds in Euclidean Spaces. — 2006. — ISBN 978-0-8218-4071-9.
- Sigurdur Helgason. Differential Geometry,Lie Groups, and Symmetric Spaces. — Academic Press, New York, 1978. — ISBN 978-0-12-338460-7.
- перевод С. Хелгасон. Дифференциальная геометрия, группы Ли и симметрические пространства. — Москва: Факториал Пресс, 2005. — (XX век. Математика и механика). — ISBN 5-88688-076-3.
- David Hilbert, Stephan Cohn-Vossen. Geometry and the Imagination. — 2nd. — New York: Chelsea, 1952. — ISBN 978-0-8284-1087-8.
- Heinz Hopf. Lectures on Differential Geometry in the Large. — Springer-Verlag, 1989. — Т. 1000. — (Lecture Notes in Mathematics). — ISBN 978-3-540-51497-8.
- An Introduction to Techmüller spaces. — Springer-Verlag, 1992. — ISBN 978-0-387-70088-5.
- Thomas A. Ivey, J.M. Landsberg. Cartan for Beginners: Differential Geometry via Moving Frames and Exterior Systems. — American Mathematical Society, 2003. — Т. 61. — (Graduate Studies in Mathematics). — ISBN 978-0-8218-3375-9.
- Howard Jacobowitz. Local Isometric Embeddings of Surfaces into Euclidean Four Space // Indiana Univ. Math. J.. — 1972. — Т. 21, вып. 3. — С. 249–254. — doi:10.1512/iumj.1971.21.21019.
- Mikhail G. Katz. Systolic geometry and topology. — American Mathematical Society, 2007. — Т. 137. — (Mathematical Surveys and Monographs). — ISBN 978-0-8218-4177-8.
- =Shoshichi Kobayashi. Induced connections and imbedded Riemannian space // Nagoya Math. J.. — 1956. — Т. 10. — С. 15–25. — doi:10.1017/S0027763000000052.
- Shoshichi Kobayashi. Theory of connections // Annali di Matematica Pura ed Applicata. — 1957. — Т. 43. — С. 119–194. — doi:10.1007/BF02411907.
- Shoshichi Kobayashi, Katsumi Nomizu. Foundations of Differential Geometry. — Wiley Interscience, 1963. — Т. I. — ISBN 978-0-470-49648-0.
- Shoshichi Kobayashi, Katsumi Nomizu. Foundations of Differential Geometry. — Wiley Interscience, 1969. — Т. II. — ISBN 978-0-470-49648-0.
- Erwin Kreyszig. Differential Geometry. — Dover, 1991. — ISBN 978-0-486-66721-8.
- Differential Geometry: Curves - Surfaces – Manifolds. — American Mathematical Society, 2006. — ISBN 978-0-8218-3988-1.
- Tullio Levi-Civita. Nozione di parallelismo in una varietà qualunque // Rend. Circ. Mat. Palermo. — 1917. — Т. 42. — С. 173–205. — doi:10.1007/BF03014898.
- Barrett O'Neill. Elementary Differential Geometry. — Academic Press, 1997. — ISBN 978-0-12-526750-2.
- Osgood B., Phillips R., Sarnak P. Extremals of determinants of Laplacians // J. Funct. Anal.. — 1988. — Т. 80. — doi:10.1016/0022-1236(88)90070-5.
- Robert Osserman. A Survey of Minimal Surfaces. — Dover, 2002. — ISBN 978-0-486-49514-9.
- см. также Р. Оссерман. Минимальные поверхности. — УМН. — 1967. — Т. 22. — С. 55–136.
- Ian R. Porteous. Geometric Differentiation: for the intelligence of curves and surfaces. — Cambridge University Press, 2001. — ISBN 0-521-00264-8.
- Позняк Э. Г. Изометрические погружения двумерных римановых метрик в евклидовы пространства. — 1973. — Т. 28, вып. 4. — С. 47–77. — doi:10.1070/RM1973v028n04ABEH001591.
- Andrew Pressley. Elementary Differential Geometry. — Springer-Verlag, 2001. — (Springer Undergraduate Mathematics Series). — ISBN 978-1-85233-152-8.
- Sacks J., Karen Uhlenbeck. The existence of minimal immersions of 2-spheres // Ann. of Math.. — 1981. — Т. 112, вып. 1. — doi:10.2307/1971131. — .
- Isadore Singer, John A. Thorpe. Lecture Notes on Elementary Topology and Geometry. — Springer-Verlag, 1967. — ISBN 978-0-387-90202-9.
- John Stillwell. Sources of Hyperbolic Geometry. — American Mathematical Society, 1996. — ISBN 978-0-8218-0558-9.
- Dirk Jan Struik. Lectures on classical differential geometry: Second Edition. — Dover, 1988. — ISBN 978-0-486-65609-0.
- Michael E. Taylor. Partial Differential Equations II: Qualitative Studies of Linear Equations. — Springer-Verlag, 1996a. — ISBN 978-1-4419-7051-0.
- Michael E. Taylor. Partial Differential Equations III: Nonlinear equations. — Springer-Verlag, 1996b. — ISBN 978-1-4419-7048-0.
- Victor A. Toponogov. Differential Geometry of Curves and Surfaces: A Concise Guide. — Springer-Verlag, 2005. — ISBN 978-0-8176-4384-3.
- Топоногов, В. А. Дифференциальная геометрия кривых и поверхностей. — Физматкнига, 2012. — ISBN 978-5-89155-213-5.
- Georges Valiron. The Classical Differential Geometry of Curves and Surfaces. — Math Sci Press, 1986. — ISBN 978-0-915692-39-2. Full text of book
- Pelham Wilson. Curved Space: From Classical Geometries to Elementary Differential Geometry. — Cambridge University Press, 2008. — ISBN 978-0-521-71390-0.
Шаблон:Кривизна Шаблон:Тензоры
Для улучшения этой статьи желательно:
|































![{\displaystyle K=-{\beta ^{2} \over ((s-\alpha )^{2}+\beta ^{2})^{2}},\,\,K_{m}=-{r[(s-\alpha )^{2}+\beta ^{2})]+\beta _{t}(s-\alpha )+\beta \alpha _{t} \over [(s-\alpha )^{2}+\beta ^{2}]^{\frac {3}{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff1ab2130e1d570ae5585c216637fb7661847192)




















































![{\displaystyle K=-{1 \over 2H}\left[\partial _{x}\left({\frac {G_{x}}{H}}\right)+\partial _{y}\left({\frac {E_{y}}{H}}\right)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa6e6e49b1e0f474132e77018b4d8a8fc78a853d)













































































![{\displaystyle \gamma \colon [a,b]\to D}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75eb47b8bf3a98ea9642a1e68f812980a9ba073f)


























































