Скрученно удлинённая четырёхугольная бипирамида

Скрученно удлинённая четырёхугольная бипирамида
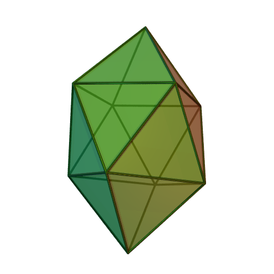(3D-модель)
Тип	многогранник Джонсона
Свойства	выпуклая, дельтаэдр
Комбинаторика
Элементы	16 граней 24 ребра 10 вершин Χ = 2
Грани	треугольники
Конфигурация вершины	2(34) 8(35)
Двойственный многогранник	square truncated trapezohedron[d]
Развёртка
Классификация
Обозначения	J17, М2+А4+М2
Группа симметрии	D4d

Скру́ченно удлинённая четырёхуго́льная бипирами́да — один из многогранников Джонсона (J₁₇, по Залгаллеру — М₂+А₄+М₂), дельтаэдр.

Составлена из 16 правильных треугольников; имеет 24 ребра одинаковой длины и 10 вершин. В 2 вершинах сходятся по четыре грани, в остальных 8 (расположенных как вершины правильной четырёхугольной антипризмы) — по пять граней.

Скрученно удлинённую четырёхугольную бипирамиду можно получить из двух квадратных пирамид (J₁) и правильной четырёхугольной антипризмы, все рёбра у которых одинаковой длины, — приложив основания пирамид к основаниям антипризмы.

Метрические характеристики

Если скрученно удлинённая четырёхугольная бипирамида имеет ребро длины $a$, её площадь поверхности и объём выражаются как

$S=4{\sqrt {3}}\;a^{2}\approx 6{,}9282032a^{2},$

$V={\frac {1}{3}}\left({\sqrt {2}}+{\sqrt {4+3{\sqrt {2}}}}\right)a^{3}\approx 1{,}4284045a^{3}.$

В координатах

Скрученно удлинённую четырёхугольную бипирамиду с длиной ребра $2$ можно расположить в декартовой системе координат так, чтобы её вершины имели координаты

• $\left(0;\;0;\;\pm \left({\sqrt {2}}+{\frac {1}{\sqrt[{4}]{2}}}\right)\right),$
• $\left(\pm 1;\;\pm 1;\;{\frac {1}{\sqrt[{4}]{2}}}\right),$
• $\left(\pm {\sqrt {2}};\;0;\;-{\frac {1}{\sqrt[{4}]{2}}}\right),$
• $\left(0;\;\pm {\sqrt {2}};\;-{\frac {1}{\sqrt[{4}]{2}}}\right).$

При этом ось симметрии многогранника будет совпадать с осью Oz, а две из четырёх плоскостей симметрии — с плоскостями xOz и yOz.

Ссылки

• Weisstein, Eric W. Скрученно удлинённая четырёхугольная бипирамида (англ.) на сайте Wolfram MathWorld.