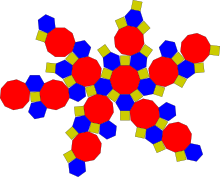
Ромбоусечённый икосододекаэдр
| Ромбоусечённый икосододекаэдр | |||
|---|---|---|---|
 (вращающаяся модель, 3D-модель) | |||
| Тип | архимедово тело | ||
| Свойства | выпуклый, изогональный | ||
| Комбинаторика | |||
| Элементы |
|
||
| Грани |
30 квадратов 20 шестиугольников 12 десятиугольников |
||
| Конфигурация вершины | 4.6.10 | ||
| Двойственный многогранник | гекзакисикосаэдр | ||
| Классификация | |||
| Обозначения | bD, taD | ||
| Символ Шлефли | tr{5,3} | ||
| Группа симметрии | Ih (икосаэдрическая) | ||
| Количественные данные | |||
| Телесный угол при вершине | |||
Ромбоусечённый икосододека́эдр[1] или усечённый икосододека́эдр[2][3] — полуправильный многогранник (архимедово тело) с 62 гранями, составленный из 30 квадратов, 20 правильных шестиугольников и 12 правильных десятиугольников.
В каждой из его 120 одинаковых вершин сходятся одна квадратная грань, одна шестиугольная и одна десятиугольная. Телесный угол при вершине равен в точности
Имеет 180 рёбер равной длины. При 60 рёбрах (между квадратной и шестиугольной гранями) двугранные углы равны при 60 рёбрах (между квадратной и десятиугольной гранями) при 60 рёбрах (между шестиугольной и десятиугольной гранями)

Название «усечённый икосододекаэдр», которое первоначально дал этому многограннику Кеплер, способно ввести в заблуждение. Дело в том, что в результате операции усечения, «срезав» с икосододекаэдра 30 четырёхугольных пирамид, можно получить лишь несколько иной многогранник, четырёхугольные грани которого — золотые прямоугольники, а не квадраты. Полученный многогранник полуправильным не является; впрочем, он изоморфен настоящему ромбоусечённому икосододекаэдру и может быть превращён в таковой при помощи небольшой деформации.
В координатах[править | править код]
Ромбоусечённый икосододекаэдр можно расположить в декартовой системе координат так, чтобы координаты его вершин были всевозможными циклическими перестановками наборов чисел
где — отношение золотого сечения.
Начало координат будет при этом центром симметрии многогранника, а также центром его описанной и полувписанной сфер.
Метрические характеристики[править | править код]
Если ромбоусечённый икосододекаэдр имеет ребро длины , его площадь поверхности и объём выражаются как
Радиус описанной сферы (проходящей через все вершины многогранника) при этом будет равен
радиус полувписанной сферы (касающейся всех рёбер в их серединах) —
Вписать в ромбоусечённый икосододекаэдр сферу — так, чтобы она касалась всех граней, — невозможно. Радиус наибольшей сферы, которую можно поместить внутри ромбоусечённого икосододекаэдра с ребром (она будет касаться только всех десятиугольных граней в их центрах), равен
Расстояния от центра многогранника до шестиугольных и квадратных граней превосходят и равны соответственно
Примечательные свойства[править | править код]
Среди всех платоновых тел, архимедовых тел и тел Джонсона с заданной длиной ребра ромбоусечённый икосододекаэдр имеет наибольший объём, наибольшую площадь поверхности и наибольший диаметр.
Среди всех платоновых тел, архимедовых тел и тел Джонсона ромбоусечённый икосододекаэдр имеет наибольшее число вершин и наибольшее число рёбер (но не наибольшее число граней — здесь первое место занимает курносый додекаэдр).
Примечания[править | править код]
- ↑ Веннинджер, 1974, с. 20, 40.
- ↑ Энциклопедия элементарной математики, 1963, с. 437, 434.
- ↑ Люстерник, 1956, с. 184.
Ссылки[править | править код]
- Weisstein, Eric W. Ромбоусечённый икосододекаэдр (англ.) на сайте Wolfram MathWorld.
Литература[править | править код]
- М. Веннинджер. Модели многогранников. — Мир, 1974.
- Многоугольники и многогранники // Энциклопедия элементарной математики. Книга четвёртая. Геометрия / Под ред. П. С. Александрова, А. И. Маркушевича, А. Я. Хинчина. — М.: Государственное издательство физико-математической литературы, 1963. — С. 382—447.
- Л. А. Люстерник. Выпуклые фигуры и многогранники. — М.: Государственное издательство технико-теоретической литературы, 1956.