Треугольная бипирамида
| Треугольная бипирамида | |
|---|---|

| |
| Тип | Бипирамида и Правильногранный многогранник J11(M3+ A5) - J12(2M1) - J13(2M3) |
| Коксетер | |
| Шлефли | { } + {3} |
| Список граней | 6 треугольников |
| Число рёбер | 9 |
| Число вершин | 5 |
| Группа симметрии | D3h, [3,2], (*223) порядка 12 |
| Группа вращений | D3, [3,2]+, (223), порядка 6 |
| Тип грани | V3.4.4 |
| Двойственный | Треугольная призма |
| Свойства | Выпуклый, гранетранзитивный |
| Развёртка | 
|
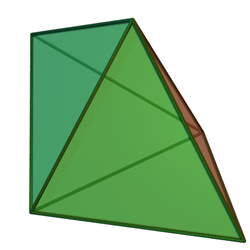
Треугольная бипирамида — вид шестигранника, первый многогранник в бесконечной последовательности гранетранзитивных бипирамид. Многогранник двойственен треугольной призме.
Как видно из имени, многогранник можно построить путём соединения двух тетраэдров по одной грани. Хотя все грани многогранника конгруэнтны и тело является изоэдральным, оно не является правильным многогранником, поскольку некоторые вершины относятся к трём граням, а другие — к четырём.
Бипирамида, шесть граней которой являются правильными треугольниками, является одним из правильногранных многогранников, (J12 в нотации Джонсона, 2M1 в нотации Залгаллера). Правильногранный многогранник является одним из 92 строго выпуклых многогранников, имеющих правильные грани, но однородным многогранником он не является (то есть многогранник не является правильным многогранником, архимедовым телом, призмой или антипризмой). Название многограннику дал Норман Джонсон, который первым перечислил эти многогранники в 1966[1]. Как правильногранный многогранник, имеющий в качестве граней правильные треугольники, он является также дельтаэдром.
Двойственный многогранник[править | править код]
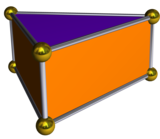
Двойственный многогранник треугольной бипирамиды — треугольная призма с пятью гранями, два параллельных правильных треугольника, связанные цепочкой из трёх прямоугольников. Хотя треугольная призма имеет вид, являющийся однородным многогранником (с квадратными гранями), двойственный многогранник правильногранного вида бипирамиды имеет прямоугольные грани, а не квадратные, так что многогранник не является однородным.
| Двойственная треугольная бипирамида | Развёртка двойственного многогранника |
|---|---|
|

|
Связанные многогранники и соты[править | править код]
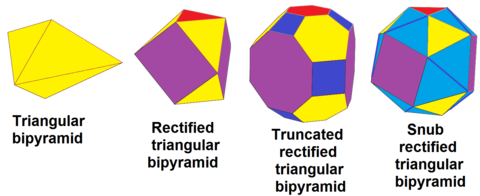
Треугольную бипирамиду dt{2,3} можно видеть в последовательности полноусечённых многогранников, rdt{2,3}, усечённых, trdt{2,3} и альтернированных (плосконосых) многогранников, srdt{2,3}:
Треугольная бипирамида может быть построена путём наращивания более мелких частей, в частности, из двух правильных октаэдров один над другим с 3 треугольными бипирамидами, добавленными вокруг сторон и по 1 тетраэдру сверху и снизу. Этот многогранник имеет 24 грани в виде правильных треугольников, но правильногранным многогранником он не является, поскольку имеет грани, находящиеся в одной плоскости (копланарные грани). Этот многогранник является копланарным дельтаэдром с 24 треугольными гранями. Этот многогранник получается путём наращивания ячеек в скрученных альтернированных кубических сотах. Бо́льшие треугольные многогранники можно получить аналогичным образом с 9, 16 или 25 треугольниками на большой треугольной грани, что можно рассматривать как часть треугольной мозаики.
Треугольная бипирамида может образовывать замощение пространства с октаэдрами или усечёнными тетраэдрами[2].
 Слои однородных четвертькубических сот можно сдвинуть с образованием пар тетраэдральных ячеек, которые комбинируются в треугольные бипирамиды. |
 скрученные тетраэдральнооктаэдральные соты имеют пары смежных правильных тетраэдров, которые можно рассматривать как треугольные бипирамиды. |
См. также[править | править код]
| Многогранник | 
|

|

|

|

|

|
||||
|---|---|---|---|---|---|---|---|---|---|---|
| Мозаика | 
|

|

|

|

|

|

|

|

|

|
| Конфигурация | V2.4.4 | V3.4.4 | V4.4.4 | V5.4.4 | V6.4.4 | V7.4.4 | V8.4.4 | V9.4.4 | V10.4.4 | ...V∞.4.4 |
Примечания[править | править код]
- ↑ Johnson, 1966, с. 169–200.
- ↑ J12 honeycomb. Дата обращения: 6 марта 2018. Архивировано 16 марта 2018 года.
Литература[править | править код]
Norman D. Johnson. Convex polyhedra with regular faces // Canadian Journal of Mathematics. — 1966. — Т. 18. — С. 169–200. — doi:10.4153/cjm-1966-021-8.
Ссылки[править | править код]
- Weisstein, Eric W. Triangular dipyramid (англ.) на сайте Wolfram MathWorld.
- Conway Notation for Polyhedra Try: dP3
Для улучшения этой статьи желательно:
|