Триакисикосаэдр
| Триакисикосаэдр | |||
|---|---|---|---|
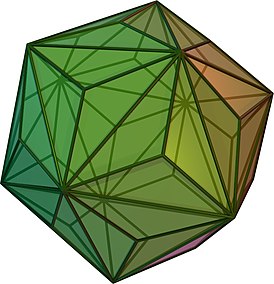 (вращающаяся модель, 3D-модель) | |||
| Тип | каталаново тело | ||
| Свойства | выпуклый, изоэдральный | ||
| Комбинаторика | |||
| Элементы |
|
||
| Грани |
равнобедренные треугольники: |
||
| Конфигурация вершины |
20(33) 12(310) |
||
| Конфигурация грани | V3.10.10 | ||
| Двойственный многогранник | усечённый додекаэдр | ||
| Классификация | |||
| Обозначения | kI | ||
| Группа симметрии | Ih (икосаэдрическая) | ||
Триакисикоса́эдр (от др.-греч. τριάχις — «трижды», εἴκοσι — «двадцать» и ἕδρα — «грань») — полуправильный многогранник (каталаново тело), двойственный усечённому додекаэдру. Составлен из 60 одинаковых тупоугольных равнобедренных треугольников, в которых один из углов равен а два других
Имеет 32 вершины; в 12 вершинах (расположенных так же, как вершины икосаэдра) сходятся своими острыми углами по 10 граней, в 20 вершинах (расположенных так же, как вершины додекаэдра) сходятся тупыми углами по 3 грани.
У триакисикосаэдра 90 рёбер — 30 «длинных» (расположенных так же, как рёбра икосаэдра) и 60 «коротких» (вместе образующих фигуру, изоморфную — но не идентичную — остову ромботриаконтаэдра). Двугранный угол при любом ребре одинаков и равен
Триакисикосаэдр можно получить из икосаэдра, приложив к каждой его грани правильную треугольную пирамиду с основанием, равным грани икосаэдра, и высотой, которая в раз меньше стороны основания. При этом полученный многогранник будет иметь по 3 грани вместо каждой из 20 граней исходного — с чем и связано его название.
Триакисикосаэдр — одно из шести каталановых тел, в которых нет гамильтонова цикла[1]; гамильтонова пути для всех шести также нет.
Метрические характеристики
[править | править код]Если «короткие» рёбра триакисикосаэдра имеют длину , то его «длинные» рёбра имеют длину а площадь поверхности и объём выражаются как

Радиус вписанной сферы (касающейся всех граней многогранника в их инцентрах) при этом будет равен
радиус полувписанной сферы (касающейся всех рёбер) —
Описать около триакисикосаэдра сферу — так, чтобы она проходила через все вершины, — невозможно.
Примечания
[править | править код]- ↑ Weisstein, Eric W. Графы каталановых тел (англ.) на сайте Wolfram MathWorld.
Ссылки
[править | править код]- Weisstein, Eric W. Триакисикосаэдр (англ.) на сайте Wolfram MathWorld.










