Пятиугольная бипирамида
| Пятиугольная бипирамида | ||
|---|---|---|
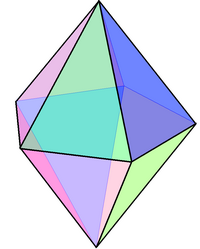 Пятиугольная бипирамида | ||
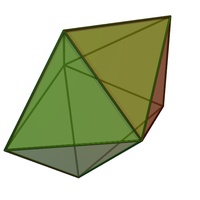 | ||
| Тип |
Бипирамида и многогранник Джонсона J12- J13 – J14 |
|
| Свойства |
выпуклый, изоэдральный (дельтаэдр) Диаграмма Коксетера: |
|
| Комбинаторика | ||
| Элементы |
|
|
| Грани | 10 треугольников | |
| Двойственный многогранник | пятиугольная призма | |
| Классификация | ||
| Символ Шлефли | { } + {5} | |
| Группа симметрии | D5h, [5,2], (*225), порядок 20 | |
Пятиугольная бипирамида (или дипирамида) — третье тело в бесконечном семействе изоэдральных бипирамид. Каждая бипирамида является двойственным многогранником для однородных призм.
Хотя тело является изоэдральным, оно не является правильным, поскольку в некоторых вершинах сходятся четыре грани, в других — пять граней.
Свойства
[править | править код]Если грани являются правильными треугольниками, тело является дельтаэдром и многогранником Джонсона (J13, по Залгаллеру — 2M3). Тело можно рассматривать как две пятиугольные пирамиды (J2 = M3), соединённые по базисам.
Многогранник Джонсона — это один из 92 строго выпуклых многогранников, имеющих правильные грани, но не являющихся однородными (то есть, они не являются правильными многогранниками, архимедовыми телами, призмами или антипризмами). Многогранники названы именем Нормана Джонсона, описавшего эти многогранники в 1966 году[1].
Пятиугольная бипирамида является 4-связной, что означает, что нужно удалить четыре вершины, чтобы оставшиеся вершины не были связны. Тело является одним из четырёх 4-связных симплициальных хорошо покрытых многогранников, что означает, что все максимальные независимые множества его вершин имеют один и тот же размер. Другие три многогранника с таким свойством — это правильный октаэдр, плосконосый двуклиноид и неправильный многогранник с 12 вершинами и 20 треугольными гранями[2].

Связанные многогранники
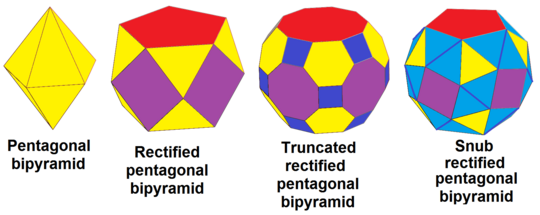
[править | править код]Пятиугольная бипирамида, dt{2,5}, принадлежит последовательности усечений — полное усечение, rdt{2,5}, усечение, trdt{2,5} и альтернация[англ.] (отсечение вершин), srdt{2,5}:
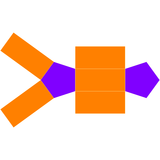
Двойственный многогранник пятиугольной пирамиды с правильными гранями (тела Джонсона) — это пятиугольная призма с 7 гранями — 5 прямоугольных граней и 2 пятиугольника.
| Двойственная пятиугольная бипирамида | Развёртка двойственного тела |
|---|---|

|
|
См. также
[править | править код]| Многогранник | 
|

|

|

|

|

|
||||
|---|---|---|---|---|---|---|---|---|---|---|
| Мозаика | 
|

|

|

|

|

|

|

|

|

|
| Конфигурация | V2.4.4 | V3.4.4 | V4.4.4 | V5.4.4 | V6.4.4 | V7.4.4 | V8.4.4 | V9.4.4 | V10.4.4 | ...V∞.4.4 |
Примечания
[править | править код]- ↑ Johnson, 1966, с. 169—200.
- ↑ Finbow, Hartnell, Nowakowski, Plummer, 2010, с. 894–912.
Литература
[править | править код]- Arthur S. Finbow, Bert L. Hartnell, Richard J. Nowakowski, Michael D. Plummer. On well-covered triangulations. III // Discrete Applied Mathematics. — 2010. — Т. 158, вып. 8. — С. 894–912. — doi:10.1016/j.dam.2009.08.002.
- Norman W. Johnson. Convex polyhedra with regular faces // Canadian Journal of Mathematics. — 1966. — Т. 18. — С. 169–200. — doi:10.4153/cjm-1966-021-8.
Ссылки
[править | править код]- Eric W. Weisstein Pentagonal dipyramid (Dipyramid) на MathWorld
- Conway Notation for Polyhedra Try: dP5
Для улучшения этой статьи желательно:
|